B.O.I. N° 79 du 29 avril 1980
III. - CANEVAS ALTIMÉTRIQUE OU NIVELLEMENT
Art. 6. - Le canevas altimétrique est un ensemble de repères déterminés en altitude par des mesures topométriques.
Art. 7. - Les tolérances relatives aux travaux de nivellement sont fixées comme suit :
A. Nivellement direct (géométrique)
1. Fermeture en altitude d'un cheminement géométrique.
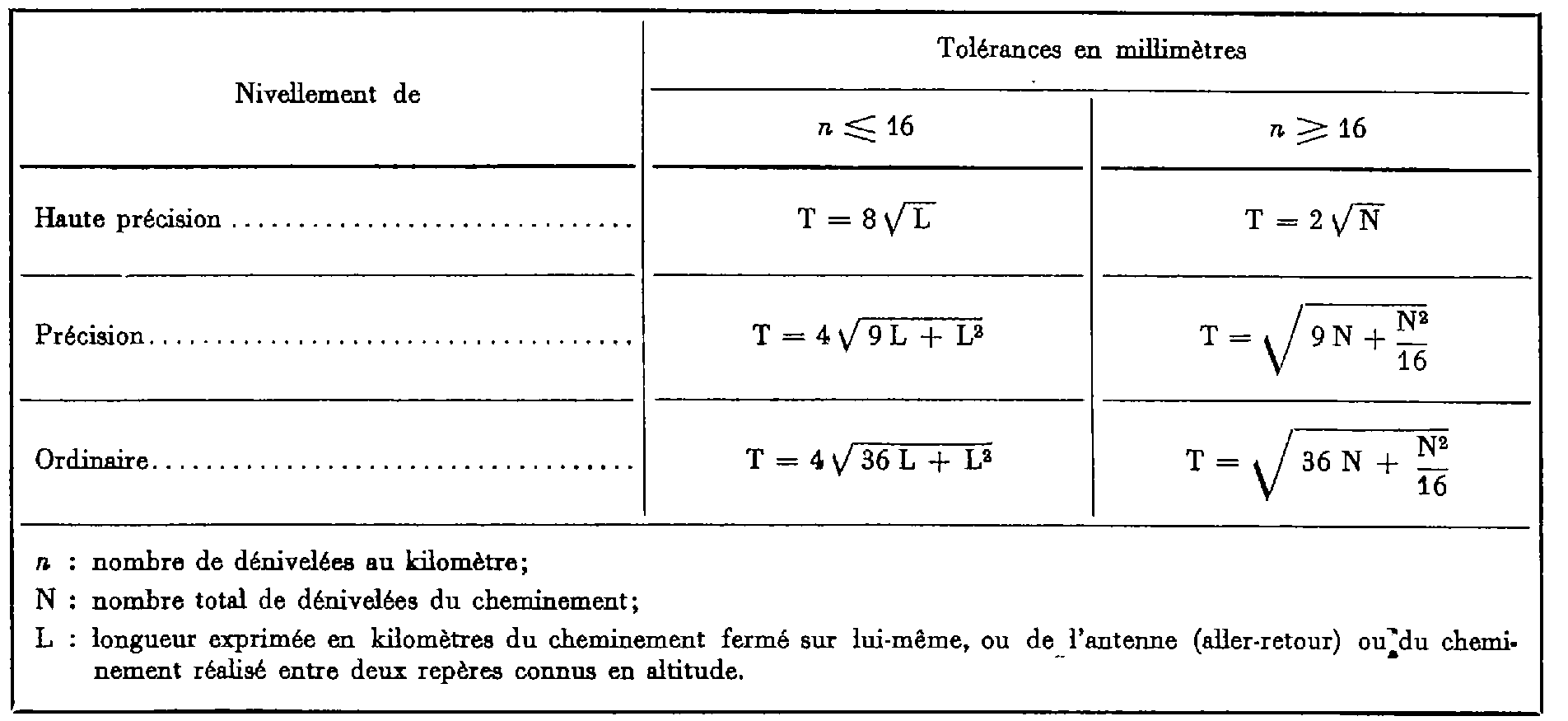
2. Point nodal (cf. art. 3, § 3.2.3).
B. Nivellement indirect (géodésique ou trigonométrique)
1. Dénivelées entre deux points :
a. CAS DE LA DISTANCE DÉDUITE DES COORDONNÉES.
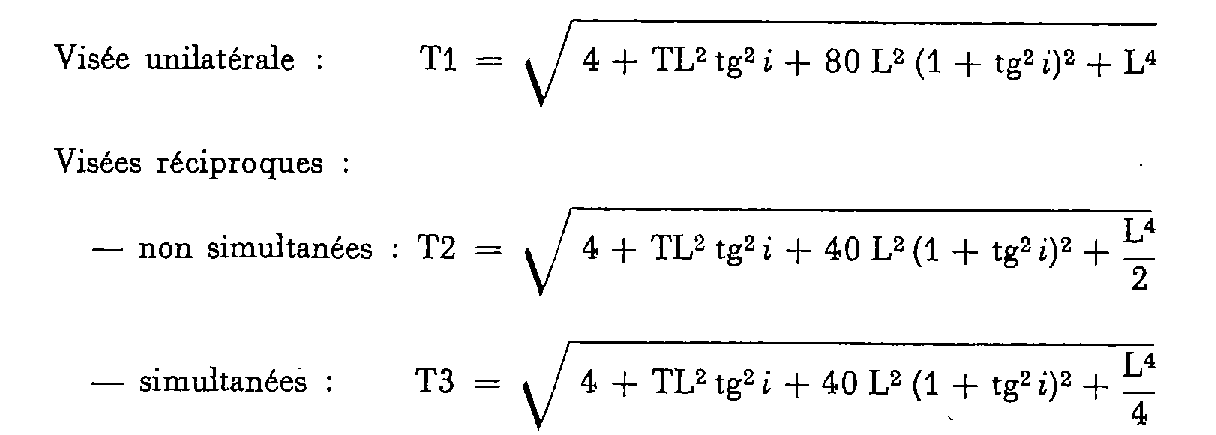
T : tolérance en centimètres ; i : angle de pente ; L : distance déduite des coordonnées et exprimée en kilomètres ; TL : tolérance en centimètres sur la distance déduite des coordonnées.
b. CAS DE LA DISTANCE MESURÉE SUIVANT LA PENTE.
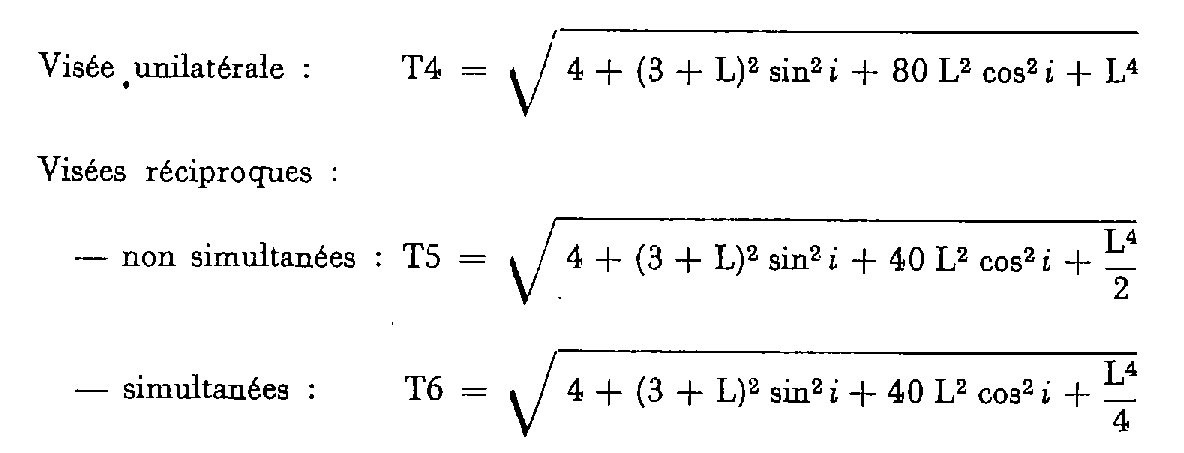
T : tolérance en centimètres ; i : angle de pente ; L : distance mesurée suivant la pente et exprimée en kilomètres.
2. Fermeture en altitude d'un cheminement (visées réciproques obligatoires).
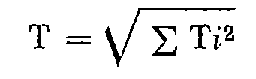
T : tolérance en centimètres ; Ti désignant la tolérance (cf. : dénivelées entre deux points) relative à chaque couple de visées réciproques (simultanées ou non simultanées), ainsi que la tolérance altimétrique des points de départ et d'arrivée du cheminement.
3. Point nodal (cf. art. 3, § 3.2.3).
IV. - TRAVAUX PHOTOGRAMMÉTRIQUES
Art. 8. - Les tolérances relatives aux travaux photogrammétriques préalables au levé de détail sont fixées comme suit :
A. Prise de vues
1. Qualité du film.
Stabilité dimensionnelle et planéité.
Moyenne des résidus de superposition par transformation affine de l'image photographique des repères du fond de chambre à la figure d'étalonnage.
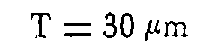
2. Exécution du vol.
2.1. RECOUVREMENT STÉRÉOSCOPIQUE LONGITUDINAL (recouvrement entre clichés consécutifs d'une même bande). Différence entre le recouvrement effectif et le recouvrement prévu.
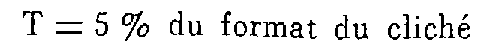
sauf à conserver un recouvrement minimal de 53 % sur toute la largeur du cliché.
2.2. RECOUVREMENT LATÉRAL (recouvrement entre bandes contiguës).
Différence entre le recouvrement effectif et le recouvrement prévu.
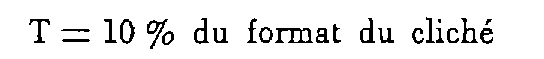
sauf à conserver un recouvrement minimal de 10 % sur toute la longueur de la bande.
2.3. CORRECTION DE DÉRIVE.
Résidu de correction de dérive.
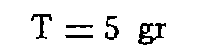
2.4. RECTITUDE APPARENTE DE L'AXE DE VOL.
2.4.1. Distance d'un point de la droite moyenne des centres de cliché à l'axe de vol prévu, lorsqu'il est imposé.

2.4.2. Distance d'un centre de cliché à la droite moyenne des centres de cliché.
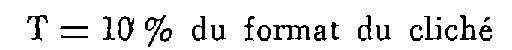
2.5. VERTICALITÉ.
Inclinaison de l'axe de prise de vues par rapport à la verticale.
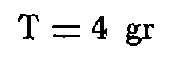
2.6. ALTITUDE.
Différence entre l'altitude théorique et l'altitude réelle.
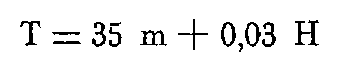
H : hauteur moyenne de vol au-dessus du sol, exprimée en mètres
B. Canevas photogrammétriques
Définition : Canevas établis en vue de travaux photogrammétriques soit par des mesures au sol, soit par des mesures sur clichés aériens. Les points de ces canevas sont toujours identifiés sur les photographies aériennes mais ils ne sont pas obligatoirement matérialisés sur le terrain.
1. Canevas de stéréopréparation.
C'est un canevas photogrammétrique établi par des mesures sur le terrain.
( Remarque : Ce canevas s'appuie sur un canevas d'ensemble qu'il peut être nécessaire de densifier ; ce complément doit alors garder les propriétés du canevas d'ensemble, donc être :
- soit un canevas d'ensemble de précision,
- soit un canevas d'ensemble ordinaire,
et ses points doivent être matérialisés au sol).
Le canevas de stéréopréparation sert à appuyer un aérocanevas ou à réaliser directement une restitution (préparation couple par couple). Ses points doivent avoir une bonne définition géométrique et photographique compatible avec les tolérances ci-après que doit respecter la détermination de leurs coordonnées :
- en position planimétrique : T = 34 × E c × 10 -6
- en altimétrie : T = (H / 5 500)
T : tolérance en mètres ;
E c : facteur d'échelle des clichés aériens (échelle = (1 / E c ) )
H : hauteur de vol au-dessus du sol, en mètres.
2. Aérocanevas.
C'est un canevas photogrammétrique établi par des mesures sur les clichés aériens. Il s'appuie soit directement sur un canevas d'ensemble, soit sur un canevas de stéréopréparation. Ses points sont des points images naturels, non matérialisés sur le terrain, ou artificiels (marques sur clichés).
2.1. ACQUISITION DES DONNÉES.
Valeurs ramenées à l'espace des clichés.
2.1.1. Parallaxe transversale résiduelle moyenne quadratique dans la formation analytique d'un modèle, estimée par la formule :
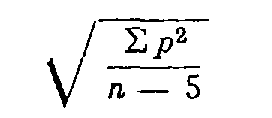
p : parallaxe résiduelle en chaque point ;
n : nombre de points à l'aide desquels a été formé le modèle (n ≥ 6).
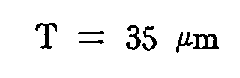
2.1.2. Écart moyen quadratique sur les points de liaisons entre deux couples d'une même bande en méthode analogique,
estimé par la formule :
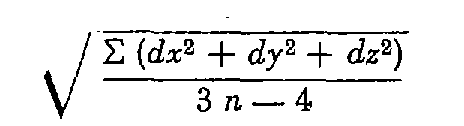
d : différence pour chaque coordonnée, entre les deux déterminations de chaque point de liaison.
n : nombre de points de liaison hormis le point de vue (n > 2).
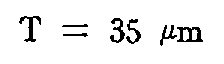
2.2. RÉSULTAT DES COMPENSATIONS.
Valeurs ramenées à l'espace des clichés.
2.2.1. Écart moyen quadratique sur les points de liaison entre bandes d'un même bloc.
Estimé par la formule :
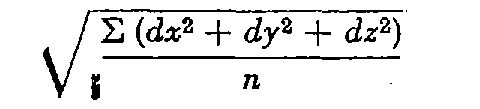
d : différence, pour chaque coordonnée, entre les deux déterminations de chaque point de liaison.
n : nombre de points de liaison.
T = 60 μm.
2.2.2. Écart moyen quadratique sur les points d'appui.
Estimé par les formules :
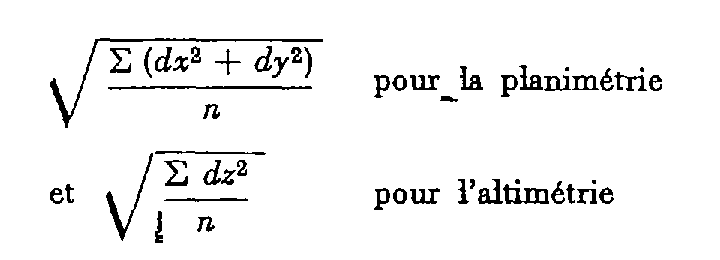
d : différence entre coordonnées terrain et coordonnées calculées de chaque point d'appui.
n : nombre de points d'appui.
- en position planimétrique T = 45 μm ;
- en altimétrie T = 30 μm.
2.2.3. Écarts individuels sur les points de contrôle.
Différence entre coordonnées terrain et coordonnées calculées de chaque point de contrôle :
- en position planimétrique T = 100 μm ;
- en altimétrie T = 65 μm.
2.2.4. Écart moyen quadratique sur les points de contrôle.
Moyenne quadratique des écarts individuels :
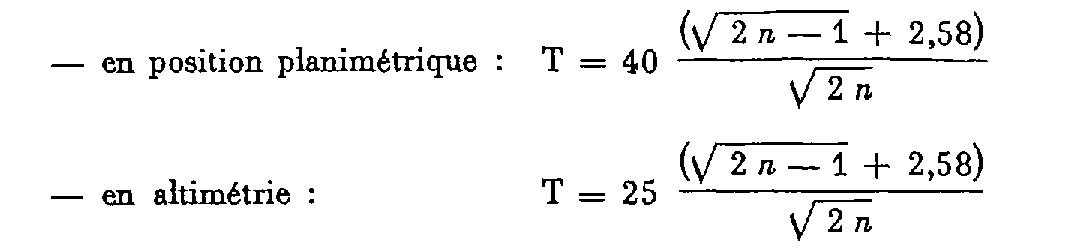
T : en μm ;
n : nombre de points de contrôle.
3. Survol couple par couple.
3.1. ÉCART RÉSIDUEL SUR LES POINTS D'APPUI.
(En position planimétrique.)
T = 22,5 + 2,25 E.
T : en centimètres.
3.2. ÉCART RÉSIDUEL MOYEN QUADRATIQUE PAR COUPLE.
(En position planimétrique.)
T = 14 + 1,4 E.
T : en centimètres.
3.3. ÉCART SUR LES POINTS A DÉTERMINATION MULTIPLE.
Écart, pour chaque coordonnée, entre la moyenne de ses déterminations et la détermination issue d'un couple.
T = 18 + 1,8 E.
T : en centimètres.
E : nombre de milliers du dénominateur de l'échelle du vol supérieur, tel que :
12 ≤ E ≤ 20.
C. Restitution (formation du modèle)
Écart individuel sur les points de calage après orientation absolue.
Différence entre coordonnées canevas et coordonnées restituées :
- en position planimétrique :
T = 0,7 Tp ;
- en altimétrie :
T = 0,5 T a .
T p : tolérance en position planimétrique exigée pour la restitution.
T a : tolérance altimétrique exigée pour la restitution.
V. - LEVER DE DÉTAIL ET VÉRIFICATION DES PLANS
Art. 9. - Les tolérances relatives au contrôle de la valeur des plans sont fixées ainsi qu'il suit :
A. Contrôle interne du levé
• Détermination multiple d'un point ou d'une longueur.
Écart entre deux déterminations indépendantes de même poids.
1. En planimétrie :
- point à détermination multiple :
T = T p ;
- longueur à détermination multiple :
T = 1,5 T p .
2. En altimétrie :
T = 1,5 Ta.
T p et T a : tolérances exigées pour le plan.
Le cahier des charges fixe le nombre de points ou de distances à déterminations multiples.
B. Vérification des plans
1. Planimétrie.
1.1. ÉCARTS INDIVIDUELS.
Catégories :
P 1 : T = 5 cm ;
P 2 : T = 10 cm ;
P 3 : T = 25 cm ;
P 4 : T = 50 cm ;
P 5 : T = 1 m ;
P 6 : T = 2,5 m ;
P 7 : T > 2,5 m.
Les plans de catégorie P 1 ou P 2 doivent être appuyés sur un canevas polygonal de précision.
1.2. ÉCART MOYEN QUADRATIQUE.
Moyenne quadratique des écarts individuels.
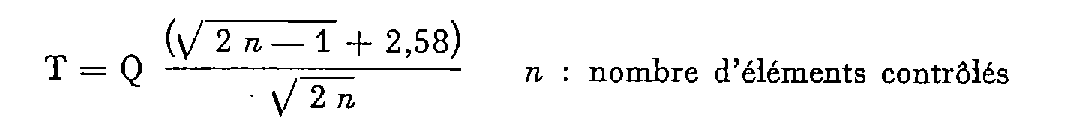
T : en centimètres.
Q : prenant, suivant la catégorie, les valeurs numériques ci-dessous.
Catégories :
P 1 : Q = 2 cm ;
P 2 : Q = 4 cm ;
P 3 : Q = 10 cm ;
P 4 : Q = 20 cm ;
P 5 : Q = 40 cm ;
P6 : Q = 1 m ;
P 7 : Q > 1 m.
2. Altimétrie. Points cotés.
2.1. ÉCARTS INDIVIDUELS.
Écart entre la cote d'un point inscrite au plan et celle issue du contrôle à partir du canevas.
Catégories
A 1 : T = 2,5 cm ;
A 2 : T = 5 cm ;
A 3 : T = 10 cm ;
A 4 : T = 25 cm ;
A 5 : T = 50 cm ;
A 6 : T > 50 cm.
2.2. ÉCART MOYEN QUADRATIQUE.
Moyenne quadratique des écarts individuels.
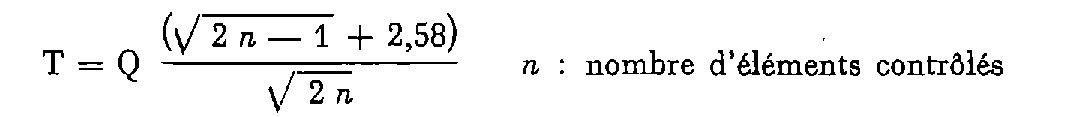
T : en centimètres.
Q : prenant, suivant la catégorie, les valeurs numériques suivantes.
Catégories
A 1 : Q = 1 cm ;
A 2 : Q = 2 cm ;
A 3 : Q = 4 cm ;
A 4 : Q = 10 cm ;
A 5 : Q = 20 cm ;
A 6 : Q > 20 cm.
3. Altimétrie. Courbes de niveau.
3.1. Écart individuel.
La tolérance s'applique à l'écart individuel réduit en fonction de l'angle de pente p, cet écart étant obtenu en divisant par (1 + 2 tg/ p /) l'écart entre la cote d'un point déduite des courbes de niveau voisines et celle issue du contrôle à partir du canevas.
Catégories :
C 1 : T = 25 cm ;
C 2 : T = 50 cm ;
C 3 : T = 75 cm ;
C 4 : T = 1 m ;
C 5 : T > 1 m.
Remarque :
Lorsque l'écart entre deux courbes de niveau est supérieur à 2 cm sur le plan, il y a lieu de tracer une courbe intercalaire.
3.2. ÉCART MOYEN QUADRATIQUE.
Moyenne quadratique des écarts individuels réduits.
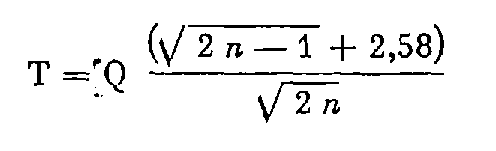
n : nombre d'éléments contrôlés.
T : en centimètres.
Q : prenant, suivant la catégorie, les valeurs numériques ci-dessous.
Catégories :
C 1 : Q = 10 ;
C 2 : Q = 20 ;
C 3 : Q = 30 ;
C4 : Q = 40 ;
C 5 : Q > 40.
Art. 10. - L'arrêté interministériel du 24 février 1951 fixant les tolérances applicables aux levés à grande échelle entrepris par les services publics est abrogé.
Art. 11. - Le présent arrêté sera publié au Journal officiel de la République française.
Fait à Paris, le 21 janvier 1980.
INSTRUCTION DU 28 JANVIER 1980
I. - CANEVAS D'ENSEMBLE
A. Observations
Les observations en une station obéissent aux conditions suivantes :
- dans chaque séquence, la référence est visée à l'ouverture et à la fermeture ; la lecture brute retenue est la moyenne des valeurs de ces deux visées ;
- dans chaque séquence, les lectures sur les différentes directions sont ensuite réduites à la référence (lecture ramenée à zéro sur la référence) ;
- les séquences sont réalisées par paires (retournement de la lunette et décalage du limbe). Pour une paire, la valeur d'une direction est la moyenne des valeurs résultant des deux séquences.
Par ailleurs, les tolérances fixées pour le canevas de précision nécessitent un centrage forcé et un nombre de paires de séquences au moins égal à 4.
1. Fermeture des séquences.
Sur le terrain même, l'opérateur doit s'assurer que les écarts constatés pour les fermetures des séquences n'excèdent pas les tolérances. Aucun dépassement n'étant admis, les opérations doivent, le cas échéant, être reprises immédiatement. Les écarts relevés ne donnent pas lieu à un classement.
2. Écart des lectures.
La tolérance est exprimée par la formule suivante :
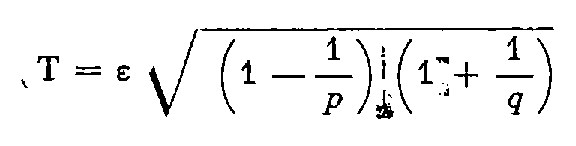
avec
ε : tolérance angulaire sur une direction ;
p : nombre de paires de séquences ;
q : poids de la référence.
La tolérance angulaire sur une direction a été déterminée à partir de travaux réels soit :
ε ≅ 1,16 mgr pour le canevas de précision ;
ε ≅ 1,5 mgr pour le canevas ordinaire.
D'où les tolérances :
Canevas de précision :
p = 4 T = 1,2 mgr ;
p = 8 T = 1,3 mgr.
Canevas ordinaire :
p = 2 T = 1,3 mgr ;
p = 4 T = 1,6 mgr.
Le poids de la référence a été pris égal à 2. Par ailleurs, les valeurs des tolérances étant très voisines pour p = 4 et p = 8, il a été retenu, pour le canevas de précision, la valeur qui correspond à p = 4. En ce qui concerne le canevas ordinaire, la tolérance correspond à p = 2, nombre de paires le plus fréquemment utilisé.
3. Écart sur la référence.
La tolérance est donnée par la formule :
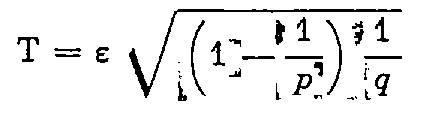
avec
p : nombre de paires de séquences ;
q : poids de la référence, égal à 2 ;
ε : tolérance angulaire sur une direction ;
D'où les tolérances :
Canevas de précision :
p = 4 T = 0,7 mgr ;
p = 8 T = 0,8 mgr.
Canevas ordinaire :
p = 2 T = 0,8 mgr ;
p = 4 T = 0,9 mgr.
Pour les mêmes raisons que précédemment, la valeur correspondant à p = 4 a été retenue pour le canevas de précision et celle correspondant à p = 2 pour le canevas ordinaire.
4. Mesure des longueurs.
Tout appareil de mesure des longueurs doit être étalonné au moins une fois par an sur une base agréée.
La tolérance sur la mesure des longueurs est de la forme généralement admise T = A + BL où A et B sont des constantes numériques déterminées par l'expérience.
Le mesurage d'une base doit être effectué au minimum deux fois avec une remise en station des instruments (mesurages indépendants).
Lorsque le procédé électromagnétique est utilisé ; les mesures doivent être exécutées avec un intervalle de temps de six heures environ entre elles.
L'ensemble des bases mesurées doit concourir à la mise à l'échelle du canevas.
B. Calculs
1. Par triangulation.
Pour un canevas de précision, les calculs doivent être exécutés en bloc par la méthode des moindres carrés.
a. FERMETURE DE LA SOMME DES ANGLES B'UN TRIANGLE.
La tolérance sur la fermeture est de la forme :
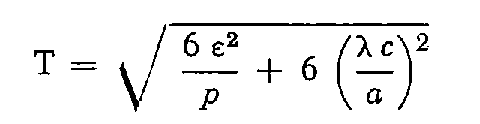
avec :
ε : tolérance angulaire sur une direction ;
p : nombre de paires de séquences ;
c : tolérance de centrage ;
a : longueur du plus petit côté du triangle ;
λ : coefficient égal à (2 / π) lorsque c est exprimé en centimètres, a en kilomètres, ε et T en milligrades.
Pour le canevas de précision, ε est égal à 1,16 milligrade et c a été fixé à 0,65 centimètre (centrage forcé) d'où la formule :
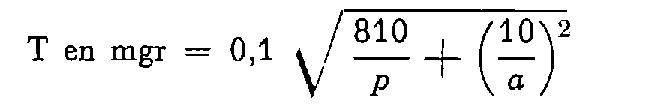
p étant pris égal à 4 on obtient la tolérance prescrite.
Pour le canevas ordinaire, ε est égal à 1,5 milligrade et la tolérance admise sur le centrage est de 3 centimètres.
D'où :
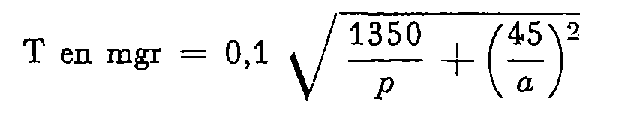
En prenant p = 2, on aboutit à la tolérance fixée.
b. ACCORD DES BASES.
La formule de tolérance retenue s'applique à un enchaînement de six à neuf triangles (cas normal) dans lesquels le plus petit angle ne doit pas être inférieur à 40 grades.
C. ÉCART D'ORIENTATION EN UNE STATION.
La tolérance sur l'écart d'orientation est exprimée par la formule :
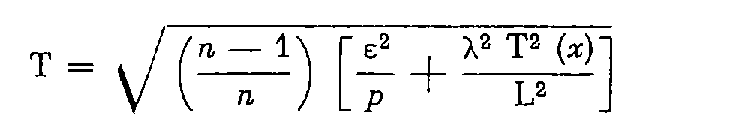
avec :
n : nombre de visées d'orientation ;
ε : tolérance angulaire sur une direction ;
p : nombre de paires de séquences ;
L : longueur moyenne des visées ;
T ( x ) : tolérance sur l'erreur en distance entre deux points du canevas ;
λ : coefficient égal à (2 / π) lorsque L est exprimé en kilomètres ;
T ( x ) en centimètres, ε et T en milligrades.
Pour le canevas de précision, ε est égal à 1,16 milligrade et T ( x ) = 4 centimètres. Par ailleurs, il a été admis que la distance moyenne des sommets du réseau était de 1,5 kilomètre. D'où la formule de tolérance correspondant à quatre paires :
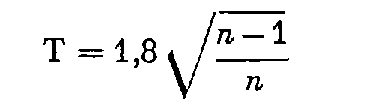
Pour le canevas ordinaire, ε est égal à 1,5 milligrade, la distance moyenne des sommets du réseau d'appui a été évaluée à 3 kilomètres. Comme T ( x ) = 20 centimètres, la tolérance pour p = 2 est égale à :
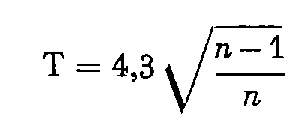
Ces tolérances varient très sensiblement en fonction de la longueur moyenne des visées.
d. ECART MOYEN QUADRATIQUE D'ORIENTATION.
La tolérance est de la forme :
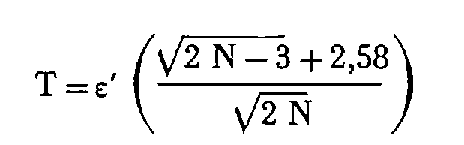
ε' se déduit des tolérances sur l'écart d'orientation et est égal à 0,7 milligrade pour le canevas de précision et 1,7 milligrade pour le canevas ordinaire.
e. ÉCART LINÉAIRE ET RAYON MOYEN QUADRATIQUE D'INDÉCISION.
Les tolérances fixées résultent du dépouillement de travaux réels.
2. Cheminements à longs côtés.
La méthode d'établissement d'un canevas par cheminements à longs côtés exige que tous les points de canevas à déterminer soient des points nodaux (trois cheminements aboutissant à chaque point).
Par ailleurs la longueur moyenne des côtés de chaque cheminement doit être supérieure à 500 mètres, aucun côté n'ayant une longueur inférieure à 200 mètres.
Enfin chaque cheminement ne doit pas comporter plus de 6 côtés dans le cas d'un canevas de précision.
Les formules de tolérances sont de la forme :
• Fermeture en orientation entre deux références successives :

n : nombre de côtés du cheminement entre les deux références d'orientation ;
t 1 et t 2 représentent, respectivement, la tolérance sur les gisements des visées d'orientation (de départ et d'arrivée) et la tolérance sur la mesure des angles du cheminement.
Canevas de précision :
t 1 = 1 mgr, ce qui correspond à une visée d'orientation de l'ordre de 2,5 km ;
t 2 = 1,4 mgr pour la mesure d'un angle de cheminement.
Canevas ordinaire :
t 1 = 5,0 mgr, ce qui correspond à une visée d'orientation de l'ordre de 2,5 km ;
t 2 = 1,4 mgr.
• Fermeture planimétrique.
La formule de tolérance est de la forme :
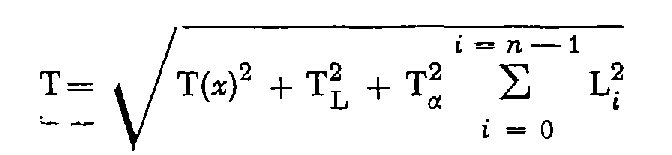
dans laquelle :
T ( x ) représente la tolérance sur l'erreur en distance entre les points de départ et d'arrivée du cheminement ;
TL est la tolérance sur la mesure des longueurs des côtés.
Elle est de la forme T l √ n , T l étant la tolérance de mesurage sur chaque côté, soit 4 cm, et n le nombre de côtés du cheminement.
Ta représente la tolérance, exprimée en radians, sur la mesure des angles du cheminement, la répartition de l'écart de fermeture angulaire ayant été effectuée.