B.O.I. N° 127 du 1 er juillet 1988

SECTION II. - CANEVAS POLYGONAL

Les modalités d'application des tolérances relatives au canevas polygonal sont identiques dans leur principe à celles développées ci-dessus dans le paragraphe 3 relatif aux calculs par cheminements à longs côtés.

Le canevas polygonal cadastral sera toujours un canevas polygonal ordinaire, quand bien même le canevas d'ensemble établi serait de précision (cf. § 1.3.).

Remarques :

1. Les mesures angulaires sont conduites en une seule paire de séquences.

2. Contrairement aux prescriptions de l'arrêté interministériel du 21 janvier 1980, dont la rédaction est entachée d'anomalie en ce qui concerne la tolérance applicable à la fermeture planimétrique des cheminements du canevas polygonal ordinaire, la formule à retenir dans ce cas est la suivante :

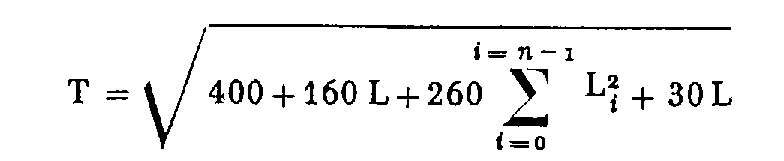
T : tolérance en centimètres.

n : nombre de côtés du cheminement.

L : longueur du cheminement exprimée en kilomètres.

Li : distance rectiligne, exprimée en kilomètres, entre le point d'arrivée du cheminement et chaque sommet (y compris le point de départ).

•

SECTION III. - CANEVAS ALTIMÉTRIQUE OU NIVELLEMENT

Le canevas altimétrique est un ensemble de repères déterminés en altitude par des mesures topométriques.

On distingue deux types de nivellement :

- le nivellement DIRECT, appelé aussi GÉOMÉTRIQUE ;

- le nivellement INDIRECT qui comporte les nivellements GÉODÉSIQUE (à longue portée) et TRIGONOMÉTRIQUE (à courte portée).

  A. Nivellement direct

  1. Modes opératoires.

Le nivellement direct peut appartenir à l'une des trois catégories suivantes :

- nivellement de haute précision ;

- nivellement de précision ;

- nivellement ordinaire.

La méthode utilisée est celle du cheminement à courtes portées avec lecture sur mires étalonnées.

Dans le cas de nivellement de haute précision, le mode opératoire doit être choisi de manière à permettre l'élimination des erreurs à tendance systématique. À cet effet, la portée, c'est-à-dire la distance de l'appareil à la mire, ne doit pas excéder 35 m. Les deux portées d'une même dénivelée doivent être égales à plus ou moins un mètre près. En outre, on doit procéder par la méthode du cheminement « aller-retour » ou du double cheminement, sur « crapaud ».

Les travaux sont obligatoirement rattachés au réseau de nivellement général en vigueur, soit actuellement le réseau des altitudes normales I.G.N. 69 dont la densité est en moyenne d'un point pour 2 km ² (sauf en région montagneuse).

Si le nivellement direct est utilisé pour déterminer les altitudes des points du canevas de stéréopréparation, dans le cadre des travaux de remaniement avec le concours de la photogrammétrie, les tolérances à appliquer sont celles du nivellement ordinaire.

  2. Tolérances sur la fermeture en altitude d'un cheminement géométrique.

La tolérance à appliquer, selon la nature du nivellement, est donnée par le tableau suivant :

  3. Exemples.

Considérons un cheminement entre deux points A et B d'altitudes connues et distants de 2 kilomètres. Soient HA et HB l'altitude respective des points A et B et dNi les différentes dénivelées calculées.

3.1. Supposons que l'on ait cheminé de A vers B en effectuant 20 stations.

Le nombre de dénivelées au kilomètre est :

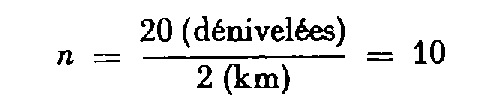
L'écart de fermeture est égal à : HB - (HA + Σ dNi). Comme n est inférieur à 16, les tolérances à appliquer sont respectivement de 19 mm et 35 mm selon qu'il s'agit d'un nivellement de précision ou d'un nivellement ordinaire.

Nota : Dans l'exemple ci-dessus, la distance moyenne entre 2 mires étant de 100 m, la portée moyenne vaut 50 m ; il n'est par conséquent pas possible de réaliser un nivellement de haute précision pour lequel toutes les portées sont inférieures à 35 m.

3.2. Supposons que l'on ait cheminé de A vers B en effectuant 40 stations telles que les distances appareil-mire aient toujours été inférieures à 35 m.

Le nombre n de dénivelées au kilomètre étant égal à 20, donc plus grand que 16, les tolérances à appliquer à l'écart de fermeture sont respectivement de 9, 14 et 27 mm, suivant la catégorie du nivellement : haute précision, précision ou ordinaire.

3.3. Pour n = 16, il y a lieu de calculer la tolérance au moyen des deux formules possibles, et de retenir la valeur la plus favorable à l'opérateur.

  B. Nivellement indirect

  1. Modes opératoires et observations.

La détermination de l'altitude d'un point par rapport à un ou plusieurs autres points connus doit être obtenue par visées réciproques. Le cahier des charges précisera s'il y a lieu de procéder par visées simultanées ou non. Lorsque cela sera possible, on préférera le cheminement à longs côtés entre deux repères d'altitude connue, qui procure une vérification.

Le nivellement d'un point par une seule visée unilatérale est formellement proscrit.

Lorsqu'un point n'est pas stationnable, rendant ainsi impossible toute visée réciproque, on utilisera pour la détermination de son altitude des visées d'intersection issues d'au moins trois points connus.

Inversement, si le point P à définir est stationnable alors que les points connus environnants ne le sont pas, on effectuera du point P des visées de relèvement sur au moins trois points.

Dans les deux cas ci-dessus, seules les visées n'exédant pas deux kilomètres seront retenues.

Chaque visée conduisant à une détermination de l'altitude cherchée, le point considéré est un point nodal, et doit dès lors être calculé comme tel.

La même méthode de calcul sera retenue en cas de recours à des visées réciproques.

Par ailleurs, l'observation des angles zénithaux suppose :

- l'utilisation d'un appareil et/ou d'une méthode permettant la mise en évidence de la collimation verticale, afin d'en éliminer les effets ;

- la réitération de chaque pointé, si possible jusqu'à l'obtention de deux lectures ne différant pas de plus de 1,0 milligrade.

  2. Tolérances.

2.1. DÉNIVELÉES ENTRE DEUX POINTS.

a. Cas de la distance déduite des coordonnées :

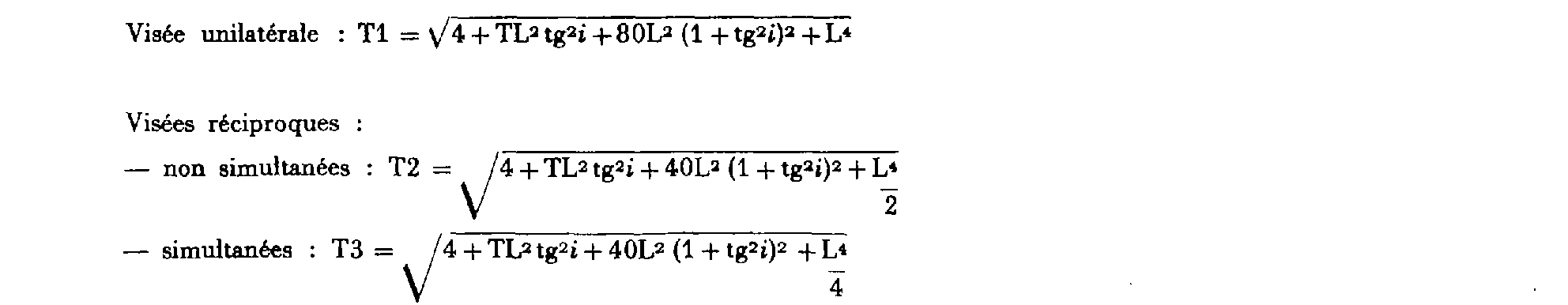
T : tolérance en centimètres ; i  : angle de pente ; L : distance déduite des coordonnées et exprimées en kilomètres ; TL : tolérance en centimètres sur la distance déduite des coordonnées, soit 4 cm pour un canevas d'ensemble de précision ou 20 cm pour un canevas d'ensemble ordinaire.

b . Cas de la distance mesurée suivant la pente :

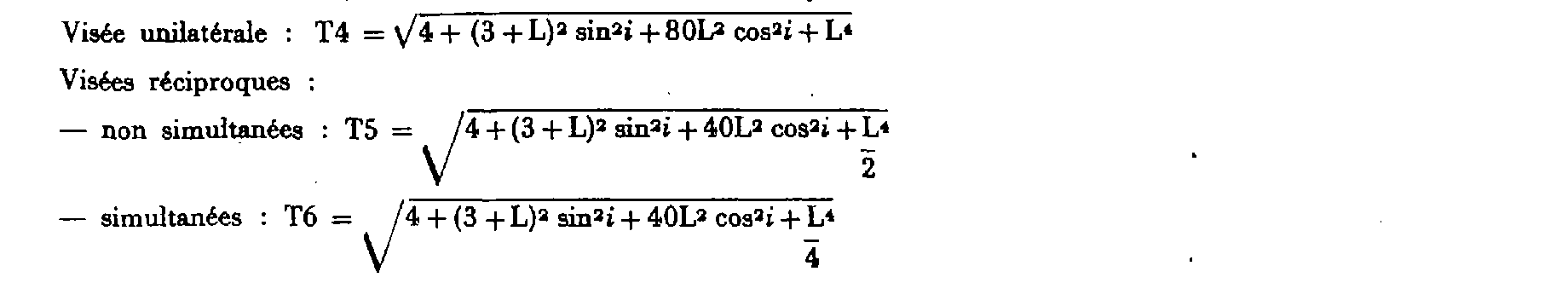
T : tolérance en centimètres ; i ; : angles de pente ; L : distance mesurée suivant la pente et exprimée en kilomètres.

2.2. FERMETURE EN ALTITUDE D'UN CHEMINEMENT (VISÉES RÉCIPROQUES OBLIGATOIRES).

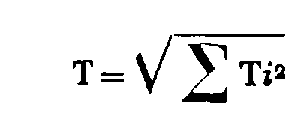
T : tolérance en centimètres ; T i désignant la tolérance (cf. : dénivelées entre deux points) relative à chaque couple de visées réciproques (simultanées ou non simultanées), ainsi que la tolérance altimétrique des points de départ et d'arrivée de cheminement.

Nota :

On retiendra pour tolérance altimétrique des points de départ et d'arrivée :

- la tolérance de fermeture des cheminements altimétriques qui ont concouru à leur détermination s'ils ont été calculés par nivellement direct ;

- la tolérance sur la moyenne pondérée T m s'ils ont été calculés par intersection, relèvement ou recoupement ;

- 20 centimètres (sauf indication contraire) pour les points géodésiques ou les points anciens pour lesquels les informations ci-dessus ne sont pas connues ;

- 0 centimètre pour les points du réseau I.G.N. 69.

  3. Exemples.

Pour tout ce qui suit nous nous placerons dans le cadre d'un canevas ordinaire. Le site des visées sera supposé réduit de repère à repère. De même les distances seront par hypothèse déduites des coordonnées, puis ramenées à l'altitude moyenne des visées et affranchies de l'altération linéaire due au système de projection.

• Visées réciproques : les erreurs de sphéricité et de réfraction sont éliminés par cette méthode. La dénivelée d N entre deux points A et B est donnée par l'expression :

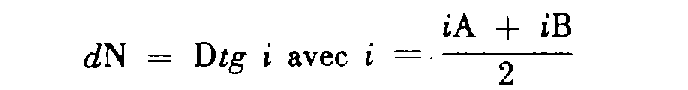
(D : distance horizontale ; i A et i B : sites des visées en A et B).

• Visées unilatérales : la dénivelée d N est donnée par l'expression :

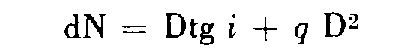
(D : distance horizontale ; i , site de la visée ; q = 0,068.10 ^-6 environ).

Exemple 1 : Détermination, par visées réciproques simultanées, de l'altitude Z _B d'un point B, à partir d'un point A d'altitude connue Z _A et de tolérance altimétrique T _A .

d'où la dénivelée : d N ₁ = + 683,17 tg 1,5192 = + 16,31 m et la tolérance s'appliquant à cette paire de visées : T ₁ = 5 cm.

Dans cet exemple où l'on n'a obtenu qu'une seule valeur de la dénivelée, la tolérance T ₁ ne donne qu'une indication sur la précision de Z _B dont la tolérance altimétrique est :

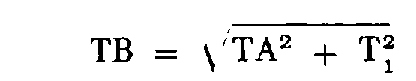
Il est souhaitable, malgré tout, que le géomètre s'assure de la cohérence des mesures de distance et de site effectuées en A et B.

• Si un autre opérateur, par exemple dans le cadre de la vérification des travaux, effectue la même paire de visées, conduisant à une dénivelée d N ₂ = + 16,37 m, l'écart d = d N ₁ - d N ₂ | = 6 cm sera comparé à la tolérance :

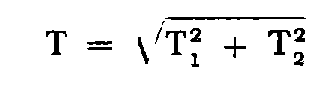
Remarques :

a. T ₂ = Ti, car la distance issue des coordonnées et l'angle trouvé par le vérificateur seront très voisins des valeurs ci-dessus.

Dans ces conditions :

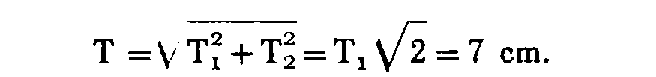
Toutefois T ₂ peut être différent de T ₁ si le vérificateur mesure la distance suivant la pente.

b. Comparer les dénivelées équivaut à comparer les deux déterminations de Z _B .

• Si le vérificateur détermine, par visées réciproques simultanées, l'altitude de B à partir d'un autre point C d'altitude connue, il ne faut plus comparer les dénivelées, mais directement les altitudes trouvées, en tenant compte de l'imprécision altimétrique des points A et C.

Soit Z' _B l'altitude du point B trouvée par le géomètre à partir du point A de tolérance altimétrique T _A et T' la tolérance d'une paire de visées réciproques (autrement dit sur la dénivelée).

Soit Z "  _B l'altitude du point B trouvée par le vérificateur à partir du point C de tolérance altimétrique T _C et T " la tolérance d'une paire de visées réciproques.

On a :

Z' _B = Z _A + DN ₁  ;

Z "  _B = Z _C + DN ₃  ;

Z' _B - Z "  _B = (Z _A + DN ₁ ) - (Z _C + DN ₃ ).

Les deux quantités entre parenthèses sont indépendantes ; par conséquent l'écart doit être comparé à :

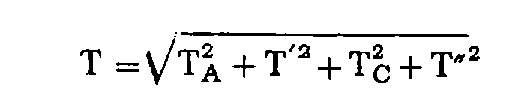
Exemple 2 : détermination, au moyen de visées réciproques simultanées, de l'altitude des points M et N appartenant à un cheminement d'extrémités A et B d'altitudes respectives Z _A et Z _B et de tolérances altimétriques respectives T _A et T _B .

On a :

- Z _A = 236,82 m et Z _B = 262,10 m, d'où d N _AB = + 25,28 m ;

- T _A = 5 cm et T _B = 10 cm ;

- AM = 518,26 m et i ₁ = 3,1234 gr, d'où d N _AM = + 25,45 m avec T _AM = 4 cm ;

- NM = 592,32 m et i ₂ = -2,9213 gr, d'où d N _MN = - 27,20 m avec T _MN = 4 cm ;

- NB = 985,64 m et i ₃ = + 1,7416 gr, d'où d N _NB = + 26,97 m avec T _NB = 7 cm.

L'écart de fermeture en altitude du cheminement AB = 25,28-(25,45-27,20+26,97)= + 6 cm est à comparer à la tolérance T ayant pour expression et valeur :

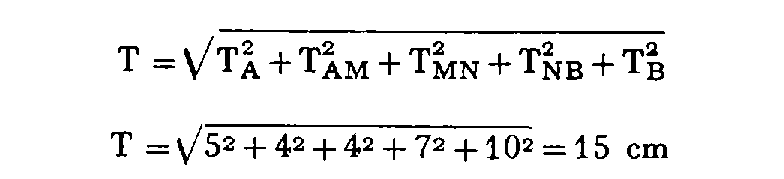
Remarque : les tolérances afférentes aux couples de visées réciproques ne sont prises en considération qu'au niveau de la tolérance sur la fermeture du cheminement.

Exemple 3 : Point nodal.

Un point nodal peut être le point de concours, soit de plusieurs cheminements, soit de plusieurs visées d'intersection, soit de plusieurs visées de relèvement, soit d'une combinaison de ces deux derniers types de visées (recoupement), soit encore d'une combinaison de l'ensemble de ces possibilités.

De manière à envisager plusieurs situations en un seul exemple, nous supposerons que le point nodal M est le point de concours d'un cheminement issu d'un point A, de visées réciproques simultanées avec un point B, et enfin d'une visée unilatérale issue d'un point C.

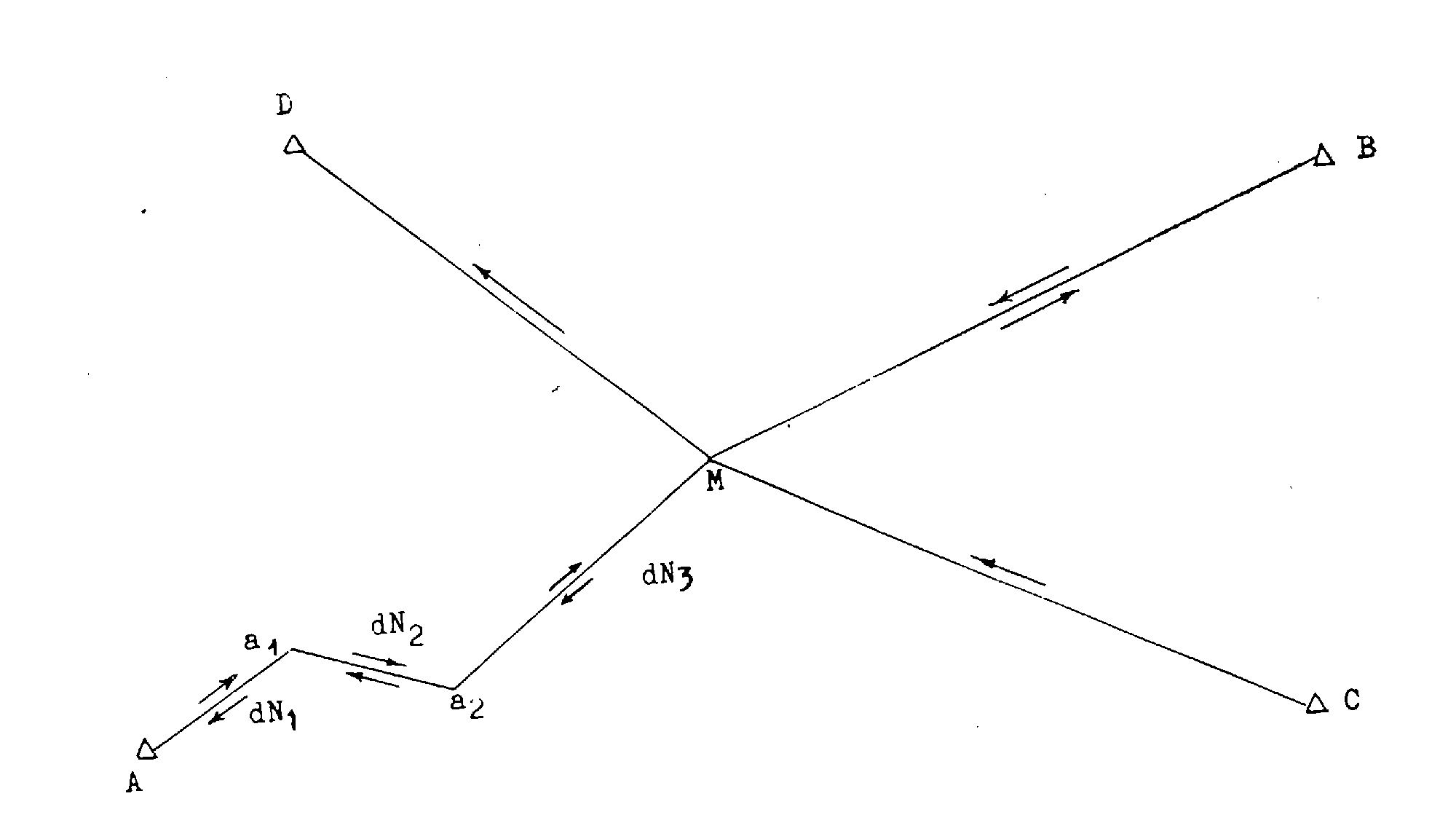
Branche AM.

Altitude de A : Z _A = 408,67 m ; tolérance altimétrique de A : T _A = 5 cm.

A a ₁ = 513,65 m et i ₁ = + 2,7694 gr ;

a ₁a ₂ = 493,24 m et i ₂ = - 8,9415 gr ;

a ₂ M = 984,12 m et i ₃ = + 1,3627 gr.

Par suite :

d N ₁ = + 22,36 m avec une tolérance T ₁ = 4 cm ;

d N ₂ = - 69,74 m avec une tolérance T ₂ = 5 cm ;

d N ₃ = + 21,07 m avec une tolérance T ₃ = 7 cm,

d'où la détermination de l'altitude de M à partir de A :

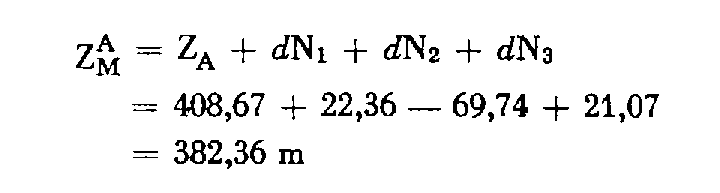
et sa tolérance :

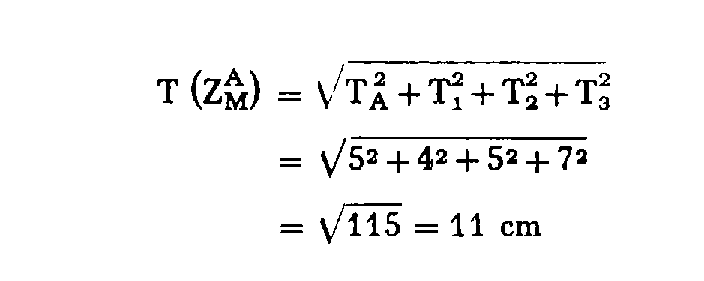
Branche BM (visées réciproques).

Altitude de B : Z _B = 311,21 m ; tolérance altimétrique de B : T _B = 5 cm.

BM = 1 960,34 m et i = + 2,3124 gr, d'où une dénivelée d N ₄ = +71,24 m de tolérance : T ₄ = 13 cm.

Par suite, l'altitude de M à partir de B :

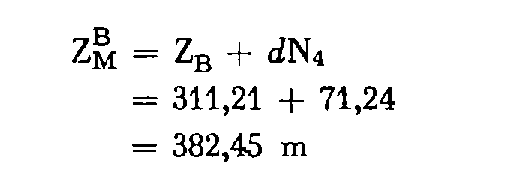
et sa tolérance :

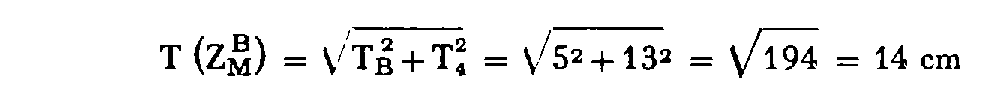
Branche CM (visée unilatérale de C sur M).

Altitude de C : Z _C = 436,69 m ; tolérance altimétrique de C : T _C = 5 cm.

CM = 1 891,38 m i = -1,8396

Par suite : d N ₅ = -54,67 + 0,24 = -54,43 m avec une tolérance : T = 18 cm :

d'où la détermination de l'altitude de M à partir de C :

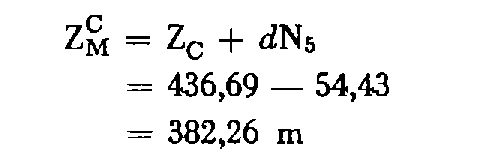
et sa tolérance :

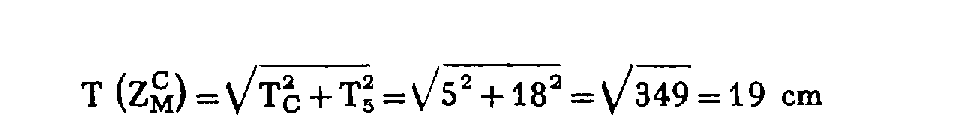
On retient pour altitude définitive du point M la moyenne pondérée Z _M des différents résultats :

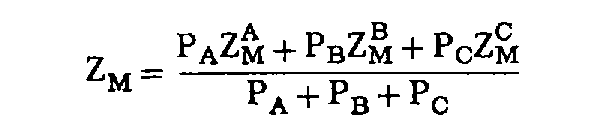
expression dans laquelle P _A , P _B et P _C sont les poids respectifs des trois déterminations de Z _M  :

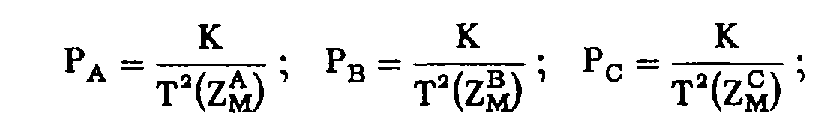
En prenant arbitrairement K = 1000, on obtient :

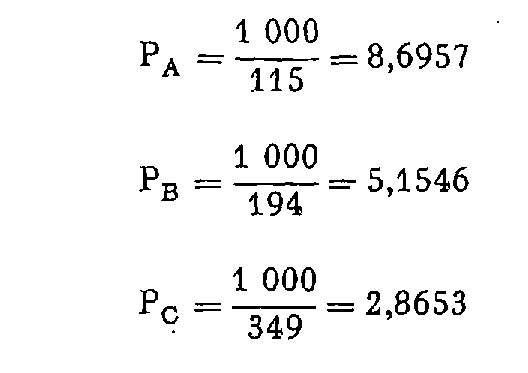
d'où

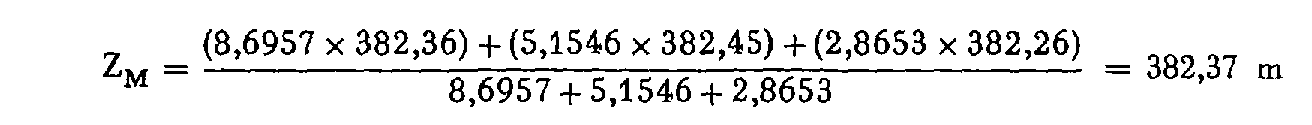
La tolérance Tm sur cette moyenne pondérée se calcule comme suit :

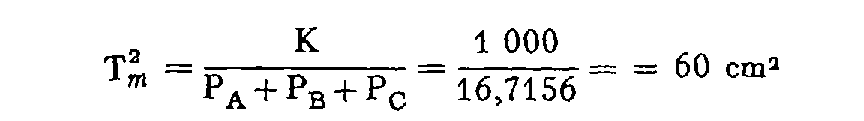
La valeur moyenne Z _M sera considérée comme acceptable si les trois conditions suivantes sont satisfaites :

Z _M - Z _M^A = 1 cm doit être inférieur ou égal à :

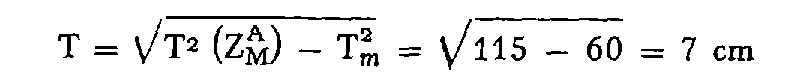
Z _M - Z _M^B = 8 cm doit être inférieur ou égal à :

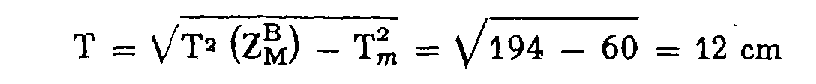
Z _M - Z _M^C = 11 cm doit être inférieur ou égal à :

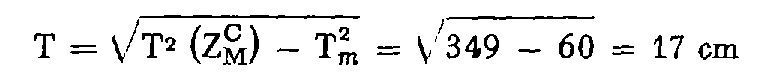
Supposons maintenant que le vérificateur des travaux effectue une visée unilatérale de M sur un point D d'altitude Z _D = 466,49 m, de tolérance altimétrique T _D = 5 cm. DM = 1 562,53 m et i = + 3,4136 gr d'où une dénivelée d N ₆ = + 83,86 + 0,17 = + 84,03 m de tolérance : T = 14 cm.

Ces observations conduisent à une quatrième détermination de l'altitude de M, indépendante des trois autres :

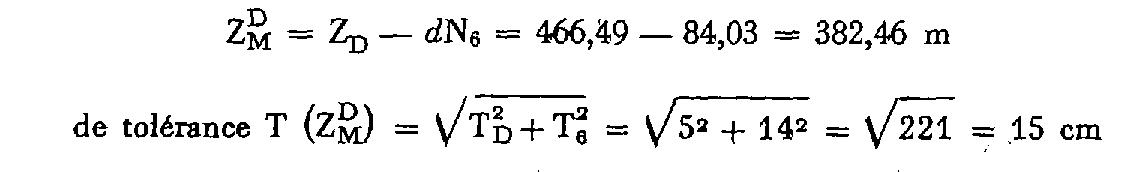
L'écart entre la valeur moyenne obtenue par le géomètre et cette détermination, soit 9 cm, doit satisfaire à la tolérance :

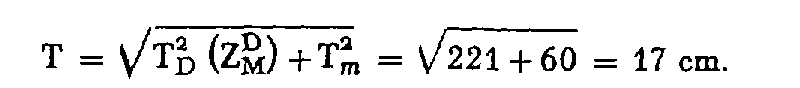
Remarque importante  : Si l'on peut comparer la valeur résultant d'une visée unilatérale de vérification à la moyenne pondérée des différentes déterminations obtenues par le géomètre, la visée de vérification pouvant d'ailleurs être la reprise d'une visée déjà effectuée par ce dernier, la comparaison directe des résultats (dénivelée ou altitude) issus d'une visée unilatérale à ceux issus d'une visée de même nature est formellement proscrite en raison des conditions d'exécution très différentes, qui pourraient rendre la tolérance inadaptée.

Par contre, les résultats issus de deux couples de visées réciproques peuvent être rapprochés sans inconvénient.

•