B.O.I. N° 127 du 1 er juillet 1988
2.6. RAYON MOYEN QUADRATIQUE D'INDÉCISION (CANEVAS ORDINAIRE SEULEMENT).
Pour chaque point calculé , il est procédé au calcul de la moyenne quadratique des écarts linéaires individuels visés au paragraphe précédent.
Ainsi un point défini par 5 visées, dont les écarts linéaires sont, respectivement, de 7 cm, 6 cm, 8 cm, 5 cm, et 7 cm, le rayon moyen quadratique d'indécision est égal à :
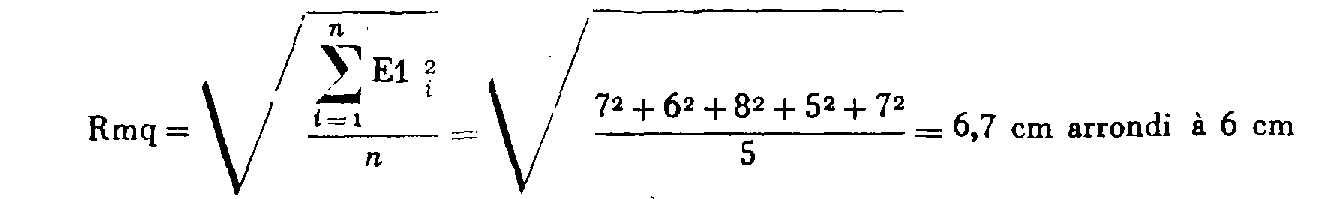
Ce résultat est à comparer à la tolérance T = 12 cm.
3. Calculs topométriques par cheminements à longs cotés.
L'instruction du 28 janvier 1980 relative à l'application de l'arrêté du 21 janvier 1980 donne les précisions suivantes :
1° La méthode d'établissement d'un canevas par cheminements à longs côtés exige que tous les points de canevas à déterminer soient des points nodaux (trois cheminements, au minimum, aboutissant à chaque point) ;
2° Par ailleurs, la longueur moyenne des côtés de chaque cheminement doit être supérieure à 500 mètres, aucun côté n'ayant une longueur inférieure à 200 mètres ;
3° Enfin chaque cheminement ne doit pas comporter plus de 6 côtés dans le cas d'un canevas de précision.
La première condition, très contraignante, pourra le cas échéant ne pas être strictement appliquée pour les canevas ordinaires présentant des difficultés de mise en oeuvre (faible densité du réseau d'appui, par exemple).
3.1. CHEMINEMENT ENTRE DEUX POINTS DE COORDONNÉES CONNUES.
3.1.1. Fermeture en orientation.
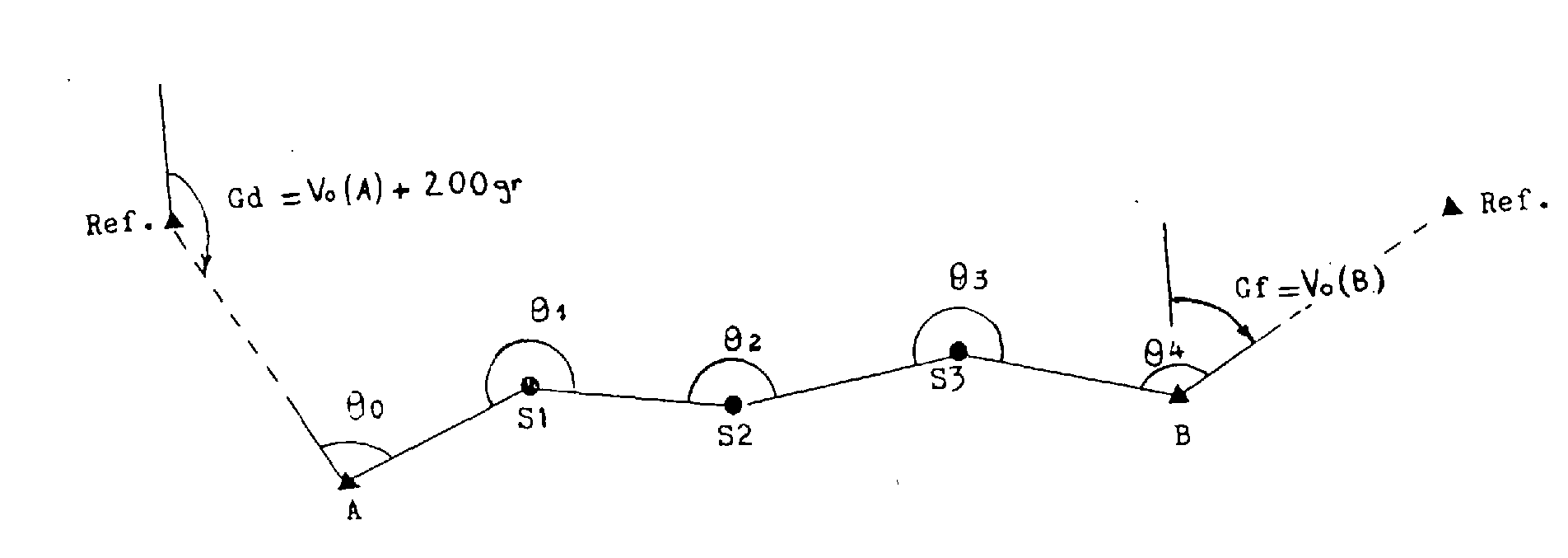
Il s'agit ici de comparer le gisement de la visée de fermeture obtenu par transmission du gisement de départ et le gisement de fermeture obtenu par calcul direct. L'écart a pour expression :
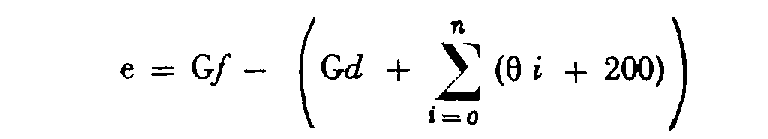
Il est à comparer à la tolérance T exprimée en milligrades :
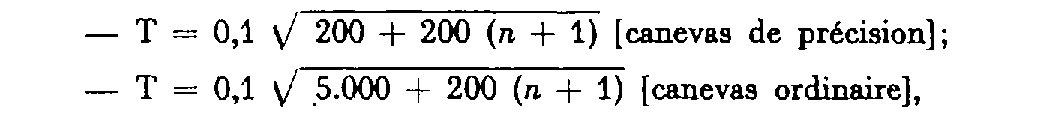
avec
n
= nombre de côtés du cheminement.
3.1.2. Fermeture planimétrique.
Il faut ici rechercher l'écart en position entre le point B sur lequel doit se fermer le cheminement et le point B' obtenu en ajoutant aux coordonnées du point de départ A, la somme des coordonnées relatives :

Les écarts en projection ont pour expression :
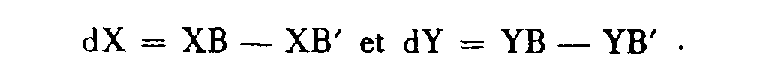
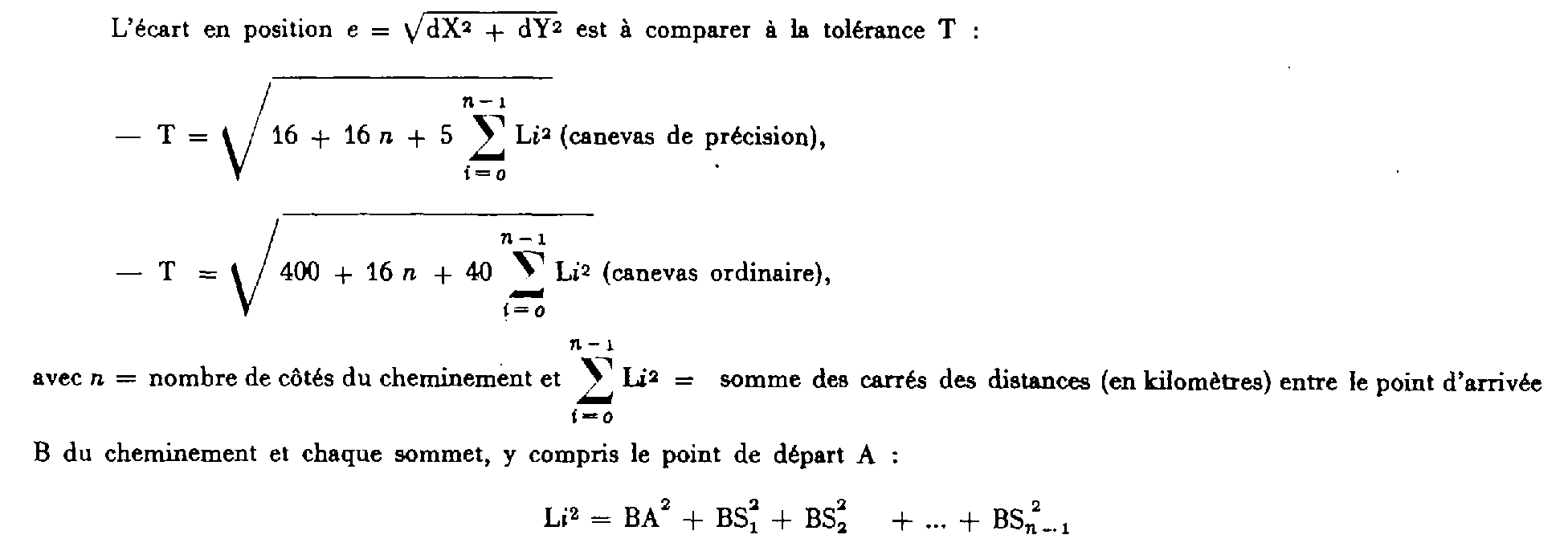
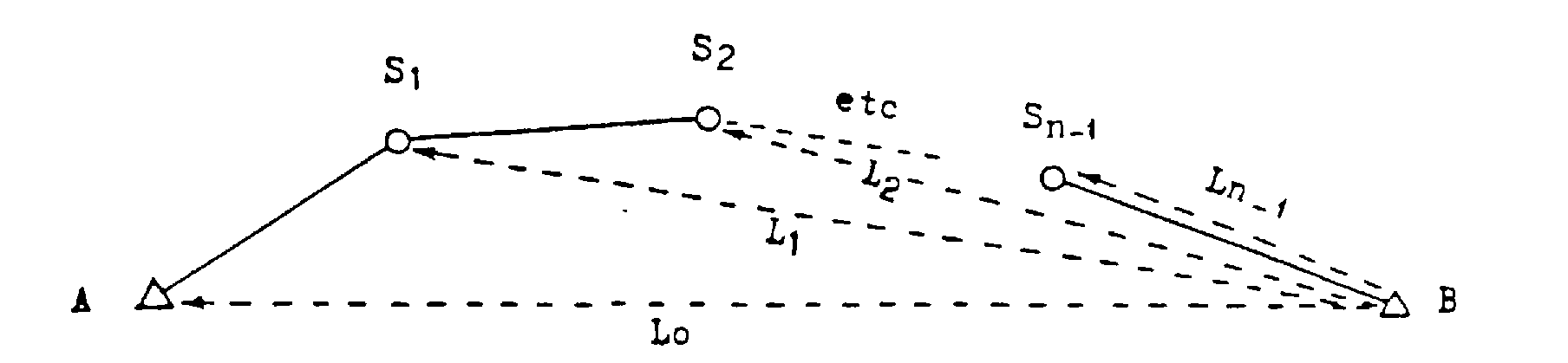
Nota : À défaut de moyens de calcul automatiques permettant le calcul direct des « Li » à partir des coordonnées, on pourra appréhender leurs valeurs avec une précision suffisante à l'aide d'un kutsch sur un croquis orienté et à l'échelle du cheminement.
Par ailleurs, la tolérance sur la fermeture planimétrique dépendant du sens de calcul du cheminement, on retiendra, si nécessaire, la valeur la plus favorable au géomètre.
3.2. POINT NODAL.
Le point nodal est défini comme le point de concours d'au moins trois cheminements. Chaque cheminement donne des coordonnées provisoires de fermeture planimétrique, X i , Y i , dont la précision de détermination peut être exprimée par Ti (Ti tolérance sur la fermeture planimétrique du cheminement considéré).
On prend pour coordonnées définitives, X et Y, du point nodal la moyenne pondérée des n déterminations :
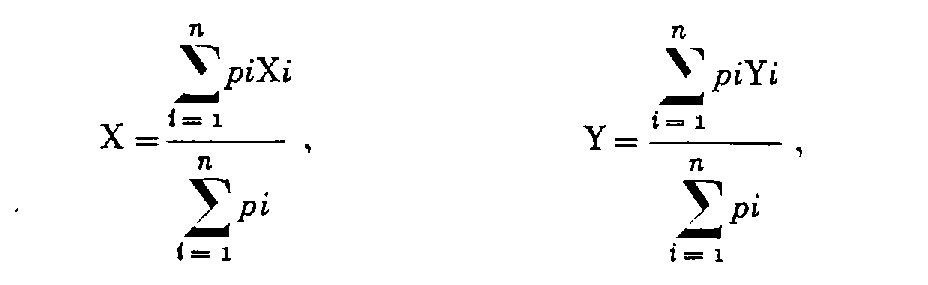
avec
pi
= (K / Ti
2
) K étant une constante arbitraire (par ex. 1000).
On démontre que la précision de la détermination du point nodal ainsi calculé s'exprime alors par la quantité T m qui vérifie la relation :
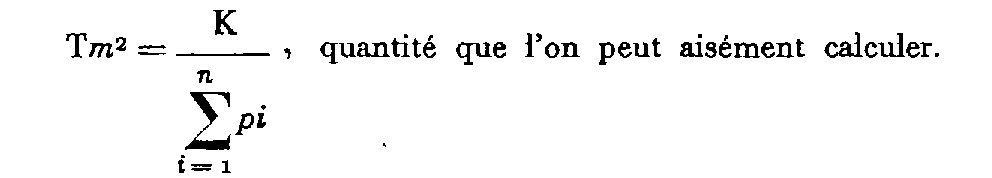
La qualité des observations et des calculs est appréciée en comparant l'écart en position entre le point définitif et chaque détermination.
Deux cas sont envisagés :
1° La détermination individuelle d'indice i est intervenue dans le calcul de la moyenne pondérée (cas général).
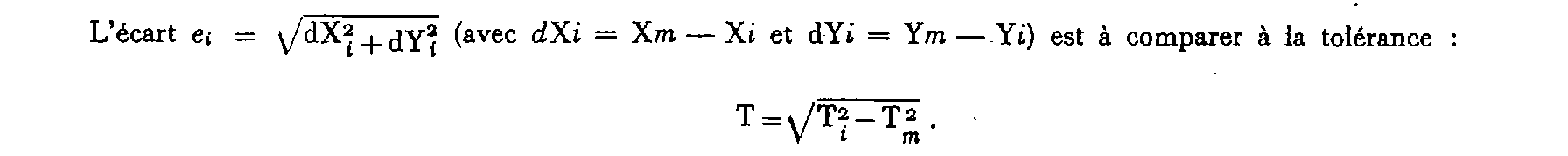
Cette opération est répétée pour chaque détermination individuelle de l'espèce, autrement dit pour tout i.
2° La détermination individuelle d'indice k n'est pas intervenue dans le calcul de la moyenne pondérée (cas par exemple d'une nouvelle détermination du point nodal par un vérificateur).
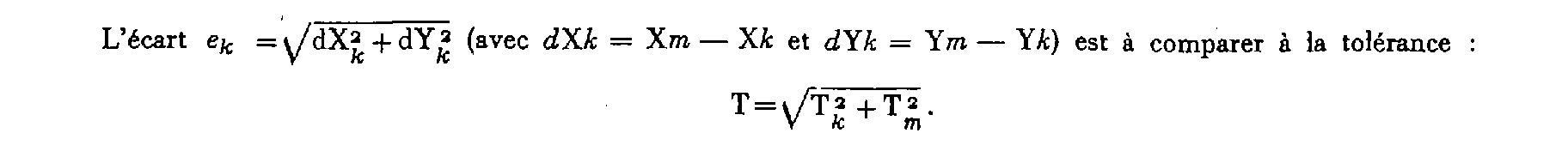
Remarque : Ces opérations peuvent être appliquées mutatis mutandis à la détermination du Vo définitif du point nodal ou du gisement définitif de fermeture choisi. (Ti est alors l'expression de la tolérance sur la fermeture en orientation entre deux références successives).
Exemple : Considérons trois cheminements ayant respectivement pour origine un point A, un point B et un point C et aboutissant en un point nodal M.
Le calcul de chacun des cheminements donne, pour M, les jeux de coordonnées provisoires suivants :
- cheminement d'origine A : X MA = 520 370,34 m Y MA = 212 674,18 m ;
- cheminement d'origine B : X MB = 520 370,37 m Y MB = 212 674,22 m ;
- cheminement d'origine C : X MC = 520 370,39 m Y MC = 212 674,25 m.
Soient TA = 15 cm, TB = 20 cm, TC = 30 cm les tolérances respectives sur la fermeture planimétrique des cheminements AM, BM, CM (cf. § 3.1., b ). Le poids de chacune des déterminations des coordonnées est :
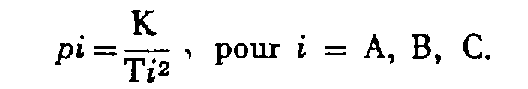
Prenons par exemple K = 3.600 ; on obtient :
- poids de la détermination issue de A : p A = (3 600 / 15 2 ) = 16
- poids de la détermination issue de B : p B = (3 600 / 20 2 ) = 9
- poids de la détermination issue de C : p C = (3 600 / 30 2 ) = 4

Les coordonnées définitives de M sont fixées à :
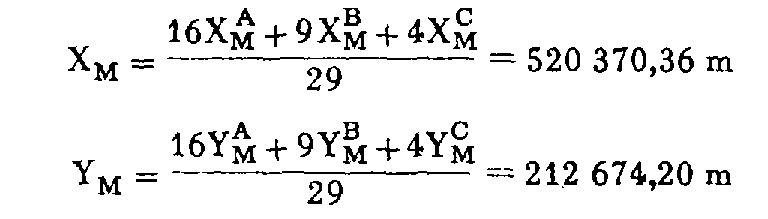
La tolérance T m sur cette détermination est telle que :
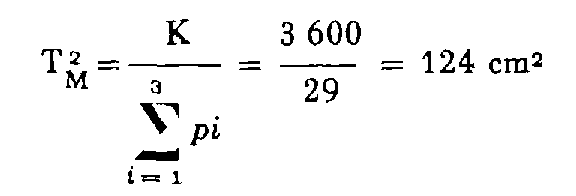
Les écarts en projection entre le point définitif M et chaque détermination ont pour valeur :
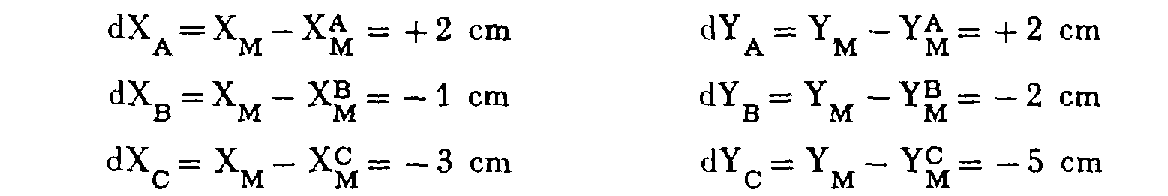
d'où les écarts en position correspondants :

Si X MD = 520 370,41 et Y MD = 212 674,26 sont les coordonnées de M obtenues par calcul d'un cheminement de vérification issu d'un point D, et dont la tolérance sur la fermeture planimétrique est TD = 10 cm,
dX D = X M - X MD = - 5 cm
dY D = Y M - Y MD = - 6 cm
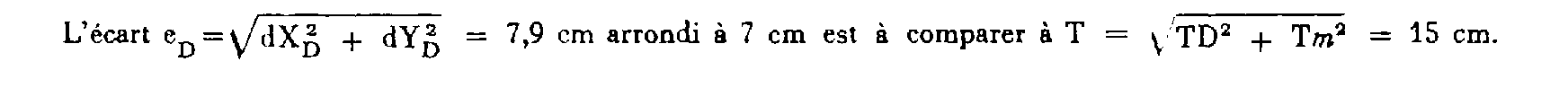
4. Auto-contrôle du géomètre.
Au fur et à mesure de l'avancement des travaux (observations, puis calculs), le géomètre doit s'assurer qu'aucun écart n'excède la tolérance.
Les anomalies constatées sur le terrain doivent, notamment, donner lieu à une reprise immédiate des observations.
Cependant, en ce qui concerne les calculs, des écarts sont parfois hors tolérance, sans pour autant compromettre la qualité des résultats requise (par exemple : écarts d'orientation afférents à des visées de faible longueur). Ces écarts ne doivent pas conduire, d'office, à une appréciation défavorable des travaux.
•