B.O.I. N° 127 du 1 er juillet 1988

  B. Application des tolérances

  1. Observations topométriques.

1.1. OBSERVATIONS ANGULAIRES EN UNE STATION.

Les observations angulaires en une station doivent satisfaire à trois types de tolérances concernant, respectivement :

- pour chaque séquence : la fermeture angulaire ;

- pour chaque direction autre que la référence : les écarts entre la lecture définitive et les lectures de paires (dits « écarts des lectures ») ;

- pour chaque paire de séquences : la somme algébrique des écarts des lectures divisée par n + 1 ( n étant le nombre de direclions visées y compris la référence). Cette valeur est appelée « écart sur la référence » de la paire considérée.

Remarque : Les textes réglementaires ne prévoient pas de tolérance spécifique applicable à l'écart constaté, au cours d'une même séquence, entre les lectures correspondant aux pointés successifs sur une même direction. Il est cependant recommandé de s'assurer que ces deux lectures ne diffèrent pas de plus de 0,5 mgr pour un canevas de précision ou de 1,0 mgr pour un canevas ordinaire. Dans l'hypothèse contraire, le pointé est réitéré jusqu'à ce que cette condition soit satisfaite.

1.1.1. Fermeture angulaire des séquences.

A chaque séquence, le point choisi comme référence est visé à l'ouverture et à la fermeture de la séquence. L'écart entre les lectures correspondant à ces deux visées sur la référence doit être inférieur ou égal à la tolérance T :

|Lecture fermeture - Lecture d'ouverture | ≤ T

La valeur de la tolérance est la suivante :

- T = 1,5 mgr (Canevas de précision) ;

- T = 2,8 mgr (Canevas ordinaire).

1.1.2. Écart des lectures.

Il s'agit, pour une direction donnée, de l'écart entre la lecture de paire et la lecture définitive. Pour un tour d'horizon comprenant un nombre p de paires de séquences, il y a p écarts de cette nature par point visé.

La valeur absolue de chaque écart de l'espèce est soumise à la tolérance suivante :

- T = 1,2 mgr (Canevas de précision) ;

- T = 1,3 mgr (Canevas ordinaire).

1.1.3. Écart sur la référence.

Il s'agit de comparer la somme algébrique divisée par n + 1 de tous les écarts de lecture d'une même paire ( n étant le nombre de directions observées y compris la référence).

Chaque écart de l'espèce, pris en valeur absolue, est soumis à la tolérance suivante :

- T = 0,7 mgr (Canevas de précision) ;

- T = 0,8 mgr (Canevas ordinaire).

Exemple : Tour d'horizon comprenant huit séquences (quatre paires) ; nombre de points observés : 5 (A, B, C, D, E) ; canevas de précision.

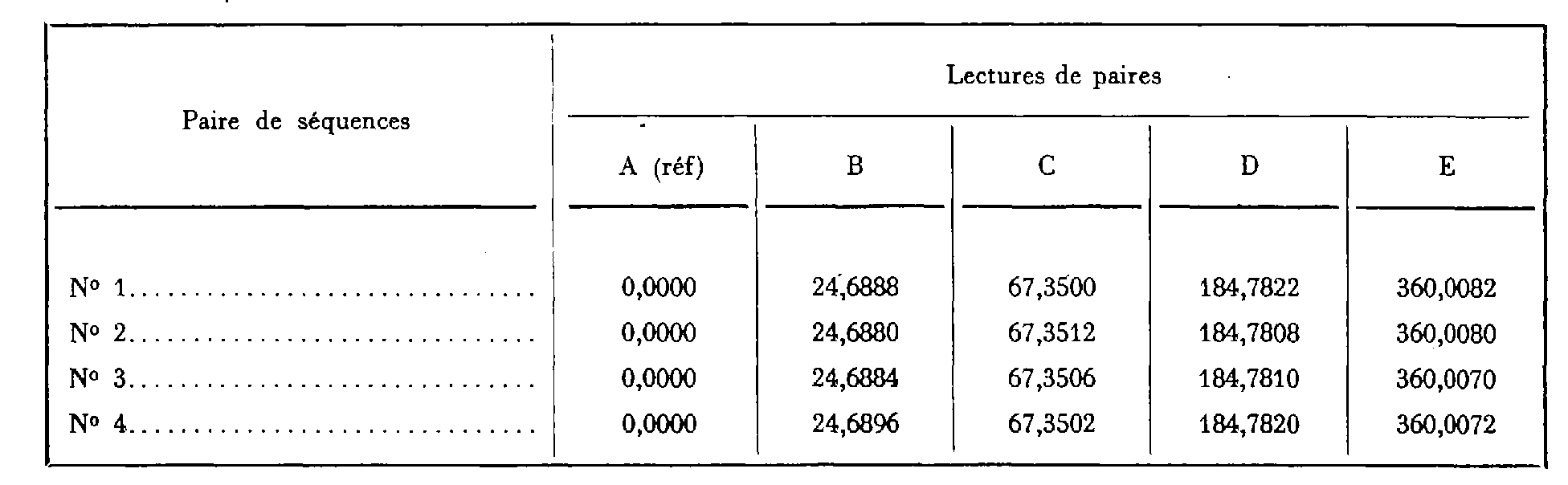
La lecture définitive retenue, pour chaque direction, est égale à la moyenne arithmétique de toutes les lectures de paires, soit :

Les écarts des lectures à comparer à la tolérance définie en 1.1.2 sont, en mgr :

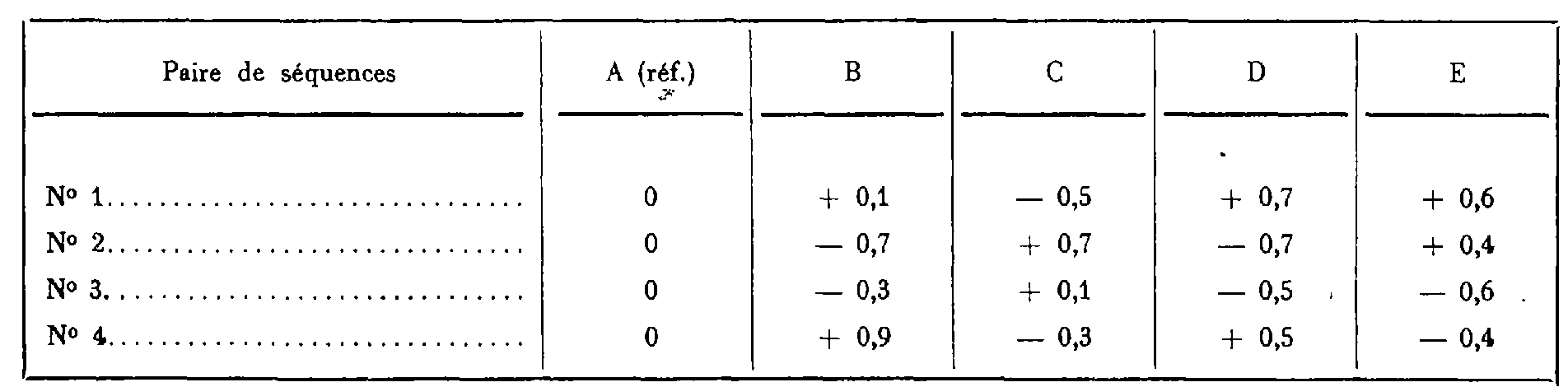
Aucune valeur absolue de ces écarts n'est supérieure à la tolérance (T = 1,2 mgr, canevas de précision).

Nota : Il convient de s'assurer que, pour chaque direction, la somme algébrique des écarts de lecture est nulle (à l'arrondissement près de la lecture définitive).

Les écarts sur la référence à comparer à la tolérance définie en 1.1.3 sont en mgr :

Aucun écart pris en valeur absolue n'est supérieur à la tolérance (T = 0,7 mgr, canevas de précision).

Nota : On peut s'assurer que pour l'ensemble des paires la somme algébrique des écarts sur la référence est nulle (à l'arrondissement près des résultats) : 0,15 - 0,05 - 0,21 + 0,11 = 0.

1.2. MESURE DES LONGUEURS.

Tout appareil de mesure des longueurs doit être étalonné au moins une fois par an sur une base d'étalonnage agréée ² .

La tolérance sur la mesure des longueurs est de la forme généralement admise T = A + BL, où A et B sont des valeurs numériques déterminées par l'expérience.

1.2.1. Mesurage de bases.

Nécessaire à la mise à l'échelle d'un canevas d'ensemble indépendant, le mesurage d'une base doit être effectué au minimum deux fois avec une remise en station des instruments (mesurages indépendants).

Lorsque le procédé électromagnétique est utilisé, les deux mesures doivent être exécutées avec un intervalle de temps de six heures environ entre elles.

L'ensemble des bases mesurées doit concourir à la mise à l'échelle du canevas.

L'écart entre deux mesurages indépendants réduits à l'horizontale ne doit pas excéder la tolérance T = 3 + L (L longueur exprimée en kilomètres et T en centimètres).

1.2.2. Cheminements à longs côtés et autres mesurages.

Sauf impossibilité, les segments seront mesurés à partir de chaque extrémité, l'écart constaté entre les deux valeurs obtenues devant satisfaire à la tolérance ci-dessus.

  2. Calculs topométriques par triangulation.

2.1. FERMETURE DE LA SOMME DES ANGLES D'UN TRIANGLE.

Certains réseaux de triangulation sont constitués par des triangles totalement observés, associés en figures géométriques simples (polygone à point central, quadrilatère, chaîne de triangles...). La mise à l'échelle peut être obtenue par le mesurage d'une ou plusieurs bases.

Dans de tels cas, il convient de s'assurer, avant d'aller plus avant dans les calculs, que satisfait aux tolérances prescrites l'écart de fermeture de la somme des angles observés de chaque triangle.

Exemple :

Soit un triangle ABC dans lequel :

- le plus petit côté du triangle mesure 2.110 m ;

- les angles observés ont pour valeur :

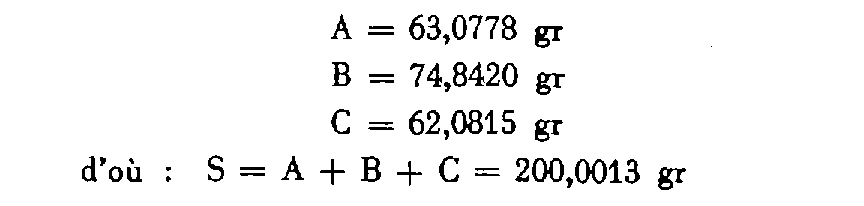
Il s'agit de comparer l'écart e = S - 200 = 1,3 mgr à la tolérance T suivante :

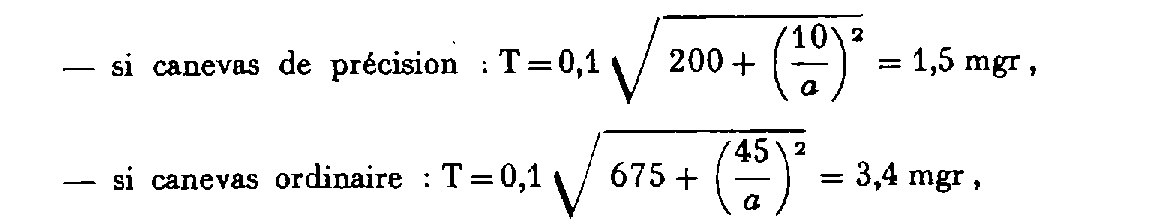
formules dans lesquelles «  a  » représente la longueur exprimée en kilomètres du plus petit côté du triangle.

2.2. ACCORD DES BASES (canevas de précision seulement).

De même, l'écart entre la mesure d'une base et sa longueur déduite de la transmission par les angles d'une autre base (éventuellement la même) ne doit pas excéder la tolérance :

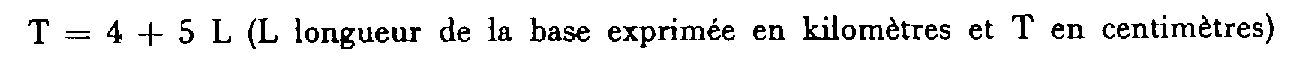
2.2.1. Cas d'une chaîne de triangles.

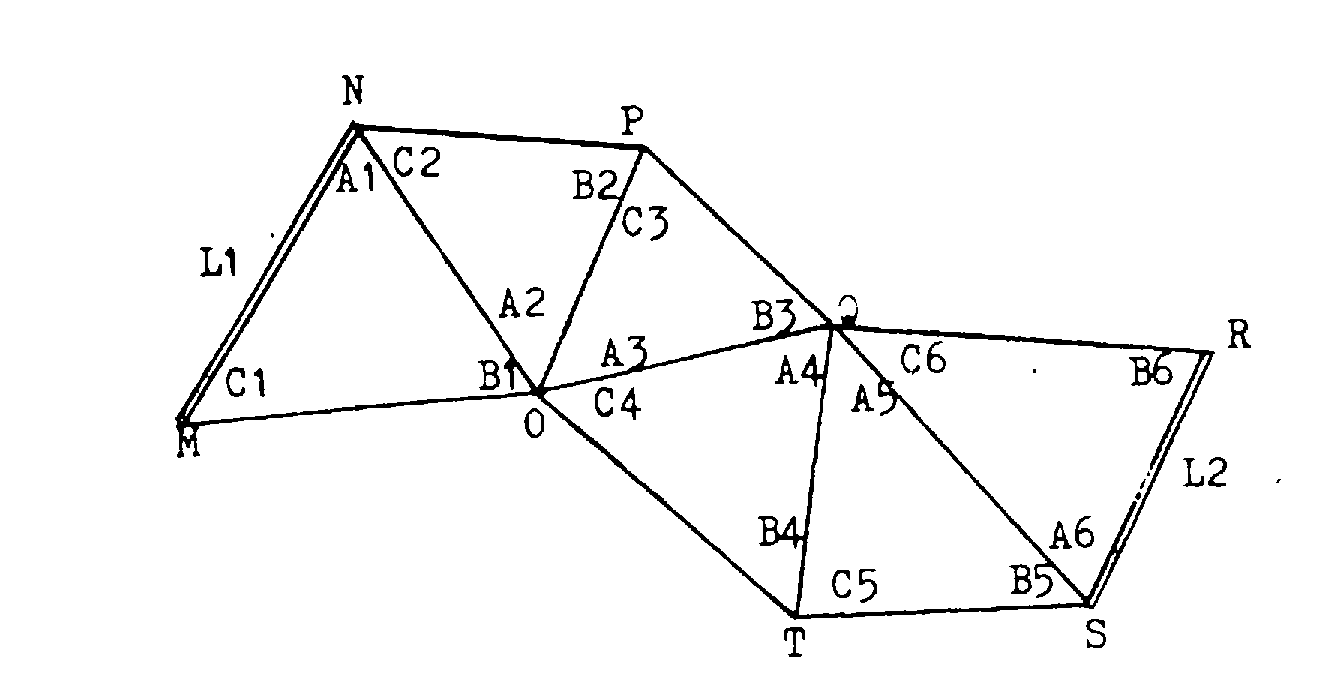
On mesure deux bases L1 et L2 situées à chacune des extrémités de la chaîne. On calcule ensuite la longueur L'2 de la base L2 par enchaînement à partir de la base L1 au moyen de l'expression :

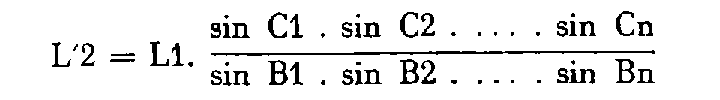
L'écart | L2 - L'2 | est alors comparé à la tolérance T ci-dessus où L est la longueur de la base L2.

2.2.2. Cas d'un polygone à point central ou d'un quadrilatère.

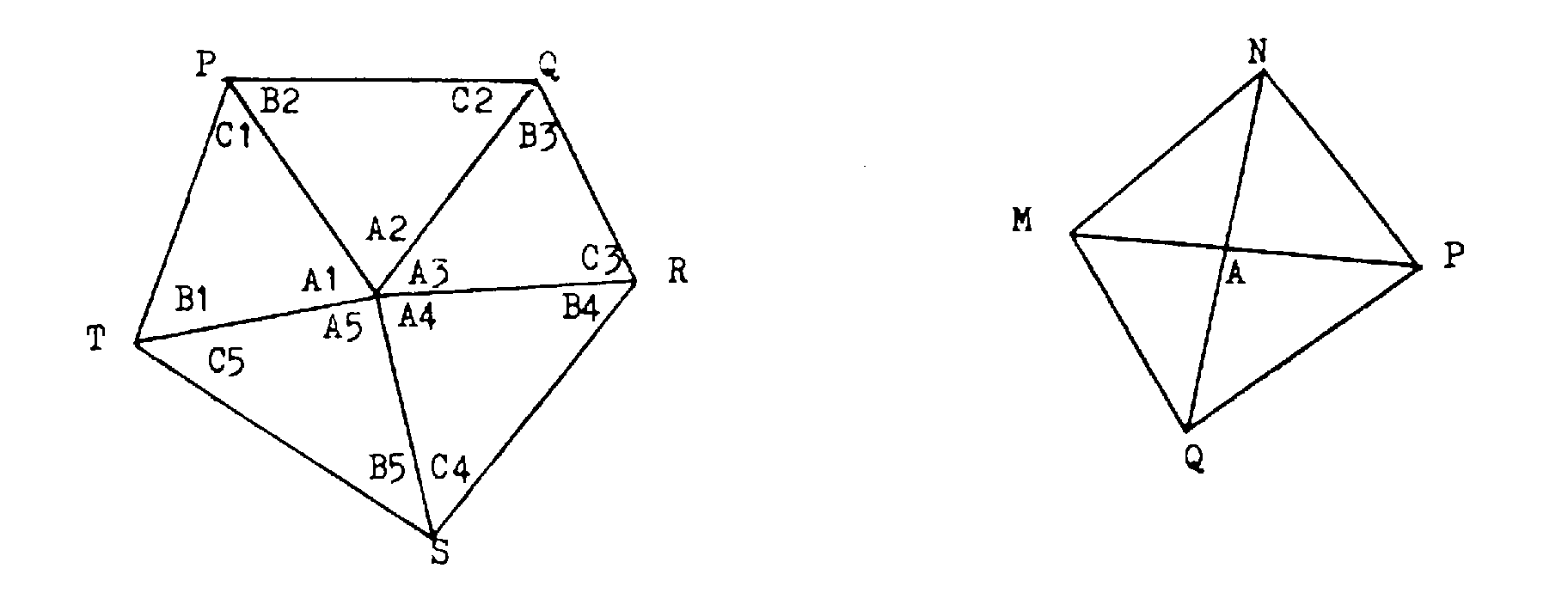
On ne mesure qu'une seule base L que l'on compare à sa valeur calculée L' transmise, par enchaînement, comme ci-dessus.

Remarque : Le canevas ordinaire étant par définition rattaché au réseau géodésique, il n'a pas été prévu de formule d'accord des bases.

2.3. ÉCART D'ORIENTATION EN UNE STATION.

2.3.1. Calcul par point isolé.

Une attention différente est à porter suivant qu'il s'agit d'une station en un point ancien ou en un point nouveau.

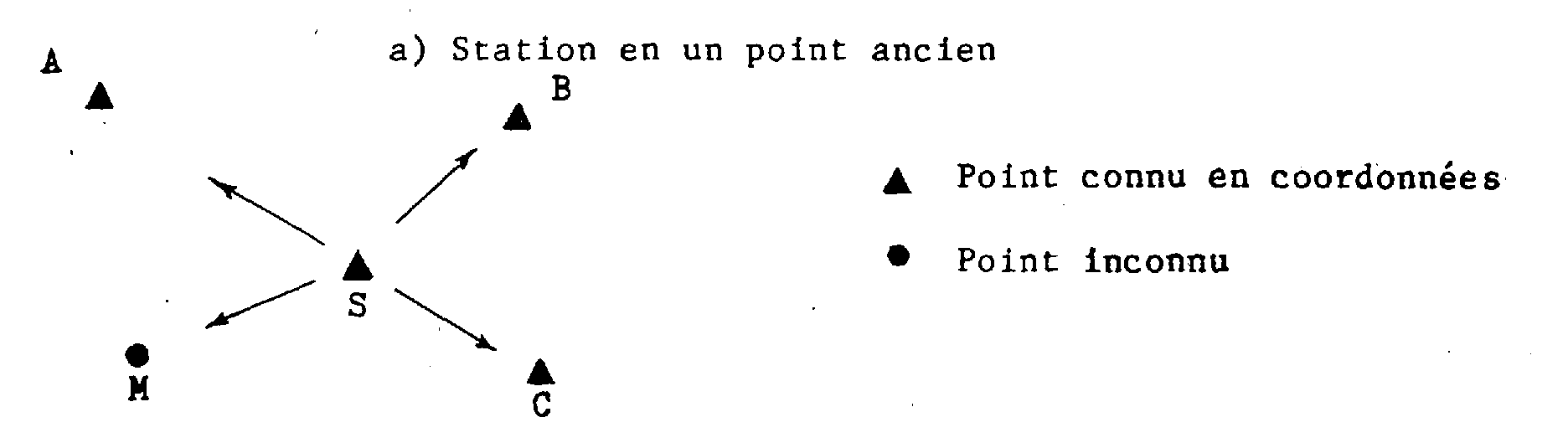
De S (point connu) ont été effectuées des visées sur A, B, C (points connus) et M (point inconnu).

Le Vo de la station S sera obtenu à partir des déterminations du Vo déduites des directions SA, SB, SC :

Vo déduit de la direction SA : V _o^A = Gc(SA) - L _A  ;

Vo déduit de la direction SB V _o^B = Gc(SB) - L _B  ;

Vo déduit de la direction SC : V _o^C = Gc(SC) - L _C  ;

(Gc = gisement calculé ; L = lecture).

On retient en principe pour Vo de la station S la moyenne arithmétique des trois Vo issus des directions SA, SB, SC :

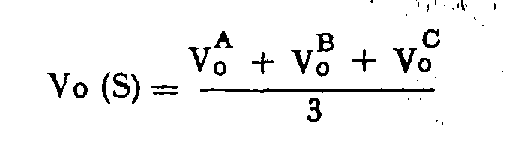
Il est possible également de calculer le Vo de la station par moyenne pondérée lorsque les longueurs des visées sont déséquilibrées, en prenant pour poids du Vo issu d'une direction la longueur de la visée correspondante.

Les écarts e _A = | Vo(S) - V _o^A |, e _B = | Vo(S) - V _o^B | et e _C = | Vo(S) - V _o^C doivent satisfaire à la tolérance :

avec n = 3 au cas de l'exemple considéré.

Connaissant le Vo de la station S, Vo(S), il est possible de déterminer le gisement observé de la direction SM qui concourra à la détermination du point M :

Lorsque les coordonnées de M seront définitivement fixées, on pourra déduire de ces coordonnées et de celles de S le gisement définitif de la direction SM : Gc(SM).

L'écart d'orientation entre le gisement observé Go(SM) et le gisement définitif Gc(SM) de la direction SM doit également satisfaire à la tolérance T ci-dessus.

Exemple : S : X = 525.378,70 m, Y = 133.749,78 m.

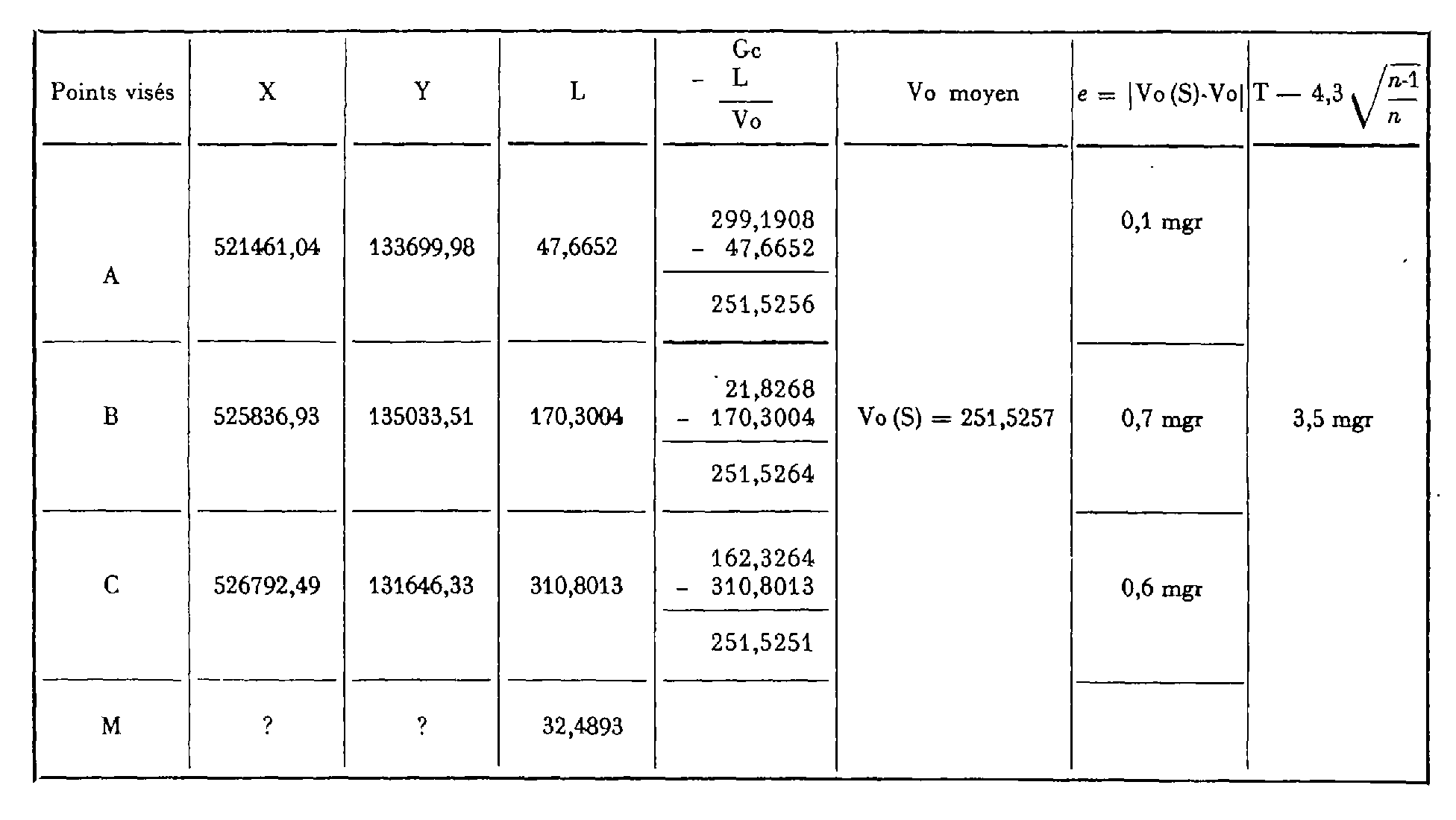
Le gisement observé de la direction SM a pour valeur :

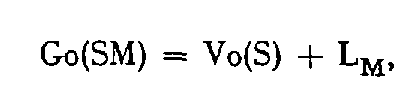
soit : Go (SM) = 251,5257 + 32,4893 = 284,0150 gr

Il contribue à la détermination des coordonnées de M.

Soit, maintenant, X _M = 524475,26 et Y _M = 133518,06 les coordonnées définitivement retenues pour le point M. On déduit de ces coordonnées et de celles de la station S le gisement définitif de la direction SM : Gc(Sm) = 284,0161 gr.

L'écart e _M = | Gc(SM) - Go(SM) | = 1,1 mgr satisfait à la tolérance T = 3,5 mgr calculée ci-dessus.

Les écarts d'orientation, relatifs à la station S sont donc :

Pour une station donnée S on obtient donc autant d'écarts que de visées effectuées sur points connus ou inconnus, la tolérance ne dépendant bien entendu que du nombre de visées sur des points connus.

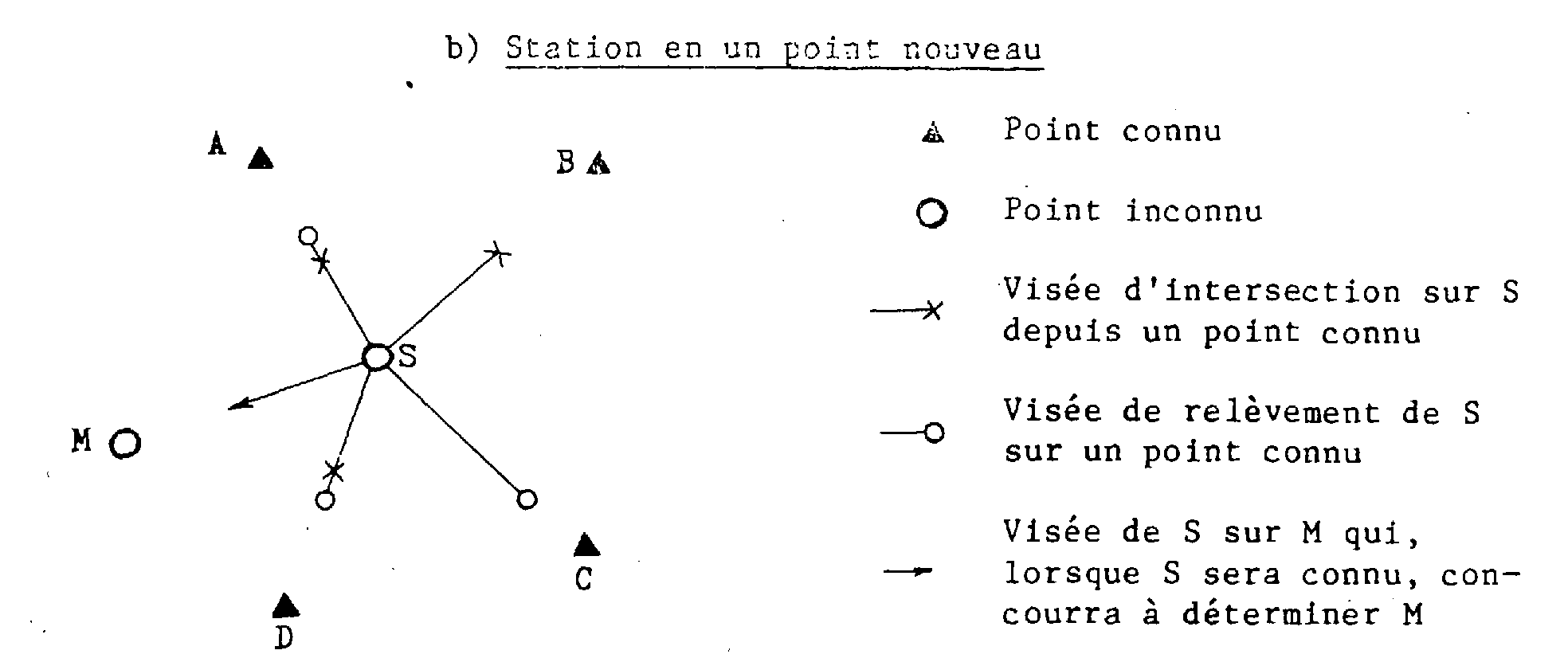
Plaçons-nous dans le cas de la détermination d'un point S par recoupement (v. fig. ci-dessus). Le Vo de la station S résulte uniquement des visées de relèvement de S sur A, C et D.

Les coordonnées approchées de S étant déterminées, on calcule un Vo approché Vo _a de la station (généralement à l'aide de la visée la plus longue observée depuis S).

Lorsque les coordonnées définitives de S sont connues, on déduit de chaque direction un Vo de station, soit par procédé numérique (Vo = G c - L), soit par procédé graphique (Vo = Vo _a ± i + 200).

Le Vo définitif Vo (S) est représenté par la moyenne de ces résultats.

À l'issue des calculs, la station S connue, devient un point ancien vis-à-vis de la détermination du point M (on se retrouve dans la situation précédente, station en point ancien). On peut donc déduire le gisement observé de SM, Go(SM), que l'on comparera au gisement définitif de SM, Gc(SM), lorsque les coordonnées de M seront connues.

L'écart e _M = | Gc(SM) - Go (SM) | devra satisfaire à la tolérance T ci-dessus.

Ainsi, une fois encore, nous aurons autant d'écarts que de visées observées depuis la station S.

2.3.2. Calcul en bloc.

À l'issue d'un calcul en bloc, les coordonnées de tous les sommets et le Vo de chaque station sont connus.

On peut alors déterminer :

- le gisement calculé Gc de chaque direction, à l'aide des coordonnées définitives des sommets ;

- le gisement observé Go = Vo + L de chaque direction, à l'aide des Vo de station définitifs, ou :

- déduire, de chaque gisement définitif, le Vo relatif à chaque direction i et le comparer au Vo définitif de station.

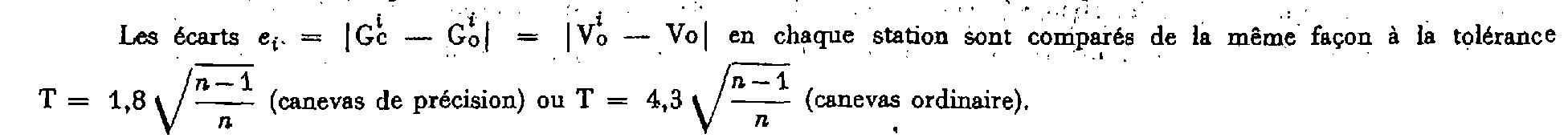
Dans tous les cas, n représente le nombre de visées d'orientation, mais il y a toujours autant d'écarts que de visées observées depuis une station donnée.

Aussi deux cas peuvent se présenter :

• Station à Vo libre : n = nombre total de visées observées depuis la station sur les points connus ou inconnus ;

• Station à Vo fixé : n = nombre total de visées d'orientation sur les seuls points connus ayant concouru à la détermination du Vo, ce nombre étant différent du nombre total de visées observées depuis la station.

2.4. ÉCART MOYEN QUADRATIQUE D'ORIENTATION.

Cet écart - unique pour un chantier donné - est la moyenne quadratique des écarts d'orientation de toutes les stations du chantier , qu'il s'agisse d'écart entre le Vo moyen et la valeur du Vo déduite de chaque visée d'orientation ou d'écart entre le gisement observé et le gisement définitif des visées d'intersection qui n'ont pas été utilisées pour l'orientation :

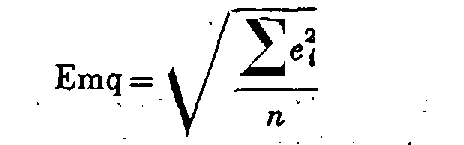
(n est égal au nombre total de visées observées pour l' ensemble des stations ).

L'écart moyen quadratique d'orientation doit être inférieur à la tolérance T, donnée en milligrades :

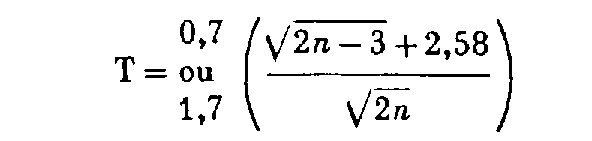
(0,7 pour un canevas de précision, 1,7 pour un canevas ordinaire).

Exemple : Soit un chantier totalisant six stations ; les écarts d'orientation (valeurs absolues) en chacune d'elles sont les suivants (en dixièmes de milligrade) :

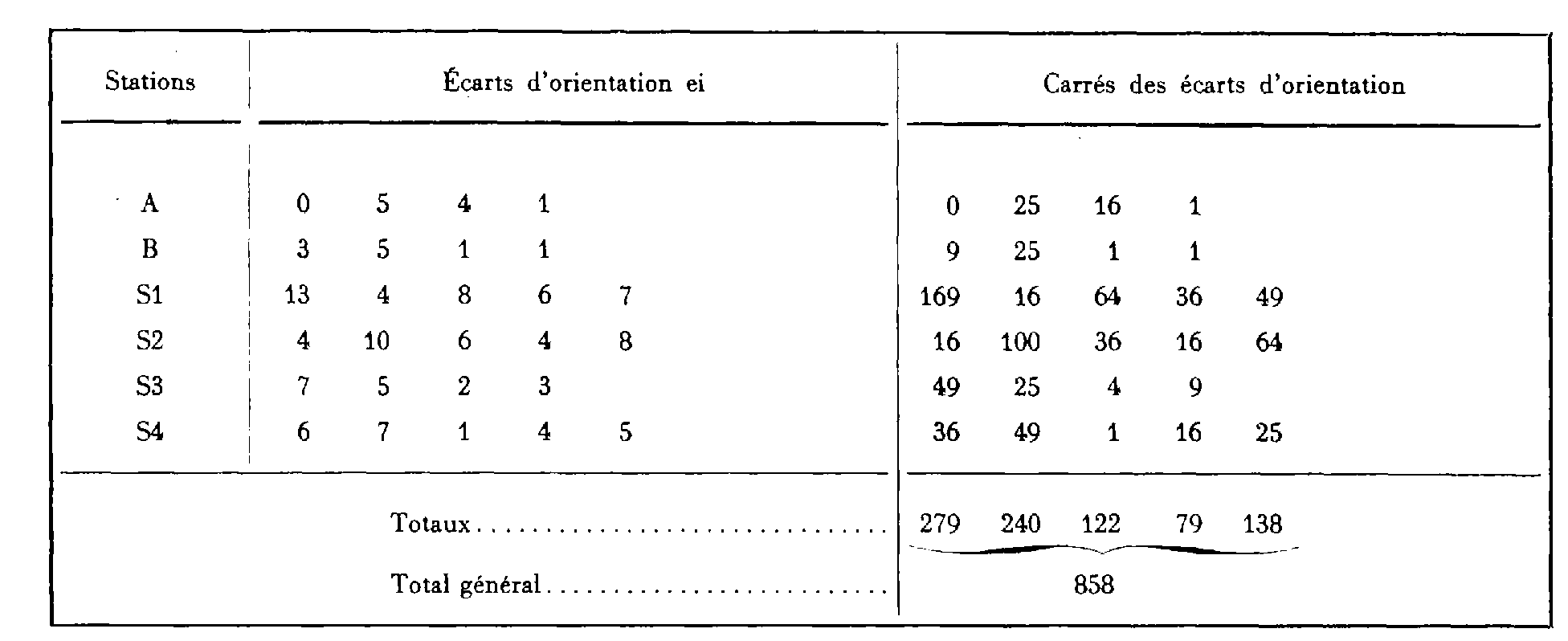
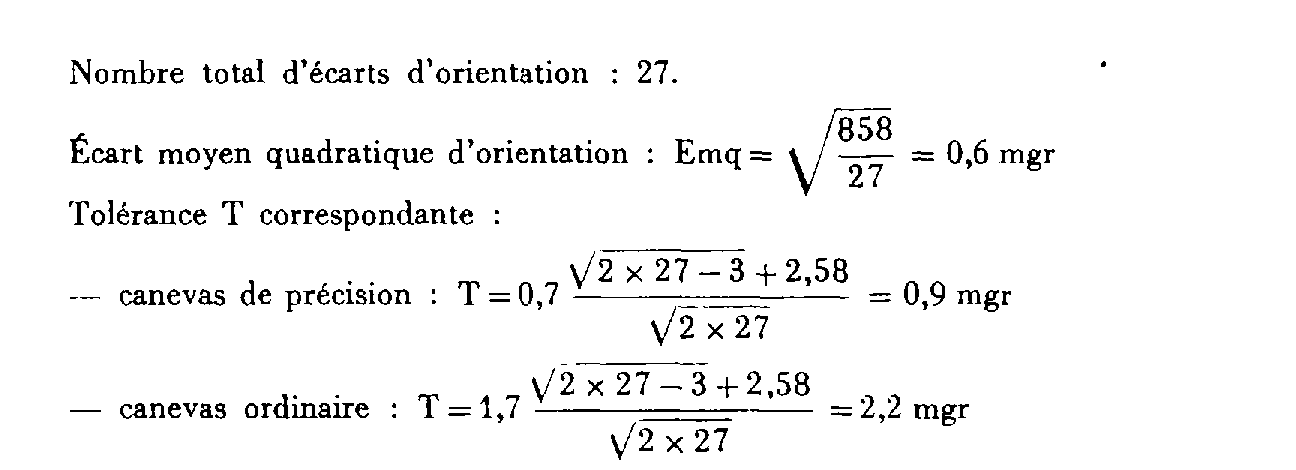
L'éventualité Emq supérieure à T traduirait que les n écarts, bien que tous individuellement inférieurs à la tolérance, ont une répartition défavorable.

2.5. ÉCART LINÉAIRE (canevas ordinaire seulement).

À chaque visée d'intersection ou de relèvement concourant à la détermination d'un point, de même qu'à chaque mesure de distance intervenant dans cette détermination le cas échéant, doit être associé un « écart linéaire », lequel représente, selon le cas :

- pour une visée d'intersection : la distance entre le point définitif et cette visée ;

- pour une visée de relèvement : la distance entre le point définitif et cette visée préalablement réorientée à l'aide du Vo définitif ;

- pour une mesure de longueur : la distance entre le point définitif et le cercle défini par cette mesure.

L'écart linéaire peut être appréhendé par des méthodes numériques ou graphiques. On emploiera la méthode la plus adéquate eu égard aux moyens mis en oeuvre pour la compensation ou le calcul de la triangulation.

Tous les écarts linéaires sont à comparer à la tolérance T = 20 cm.

• Cas n° 1. - Point déterminé par méthode numérique.

Connaissant, d'une part, les coordonnées définitives des points de départ et d'arrivée de chaque visée, d'autre part, le Vo de la station dont elle est issue, il est possible de calculer :

- le gisement définitif Gc et la longueur D, à l'aide des coordonnées ;

- le gisement observé Go = Vo + L, à l'aide du Vo définitif de la station.

L'écart linéaire E1 relatif à chaque visée a alors pour expression :

E1 = D sin dG ;

dG étant l'écart d'orientation (dG = | G o - G c |).

• Cas n° 2 . - Point déterminé par méthode graphique.

a. Intersection.

Les écarts linéaires représentent les distances, mesurées à l'échelle sur le graphique, du point définitif à chaque visée d'intersection.

b. Relèvement.

À l'aide du Vo définitif, on redétermine le gisement observé Go de chaque visée ce qui permet de calculer à quelle distance p = D sin ΔG du point approché passe chaque visée.

Un ensemble de visées parallèles aux visées « rouges » est ensuite tracé en tenant compte de ces nouvelles distances de passage.

Les écarts linéaires représentent alors les distances de passage du point définitif par rapport à ces nouvelles visées.

Autre méthode.

Connaissant l'écart dVo entre le Vo définitif et le Vo approché, il est possible de calculer la translation supplémentaire t qu'il faut imprimer à la visée « rouge » initiale pour obtenir la visée correspondant réellement aux observations :

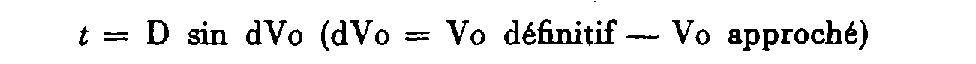
Le sens du déplacement résulte du signe de dVo :

- si dVo = Vo déf. - Vo app. est positif, la nouvelle visée « rouge » est obtenue par translation de la visée « rouge » initiale de la quantité t, à droite de la direction « point connu - point cherché » ;

- si dVo = Vo déf. - Vo app. est négatif , la nouvelle visée « rouge » est obtenue par translation de la visée « rouge » initiale de la quantité t, à gauche de la direction « point connu - point cherché ».

Les écarts linéaires sont ensuite appréhendés de la même façon que ci-dessus, en mesurant, à l'échelle du graphique, la distance du point définitif aux nouvelles visées « rouges ».

c. Recoupement.

Les écarts linéaires relatifs aux visées d'intersection et de relèvement sont calculés en combinant les méthodes ci-dessus.

• Cas n° 3 . - Point comportant, dans sa détermination, une ou plusieurs mesures de longueurs (multilatération ou insertion).

L'écart linéaire à considérer, dans ce cas, est la distance du point définitif au « lieu distance » ayant contribué à la détermination de ce point.

Si, à partir d'un point connu A, on a mesuré la distance Lm entre ce point et le point S à déterminer et si l'on appelle, par ailleurs, L c la distance résultant des coordonnées de A et des coordonnées définitives de S, l'écart linéaire E1 relatif à la mesure de longueur effectuée est :